聲子
物理名詞
聲子就是“晶格振動的簡正模能量量子”,是一種元激發。英文是phonon。
聲子就是“晶格振動的簡正模能量量子”。英文是phonon。在固體物理學的概念中,結晶態固體中的原子或分子是按一定的規律排列在晶格上的。在晶體中,原子間有相互作用,原子並非是靜止的,它們總是圍繞著其平衡位置在不斷的振動。另一方面,這些原子又通過其間的相互作用力而連繫在一起,即它們各自的振動不是彼此獨立的。原子之間的相互作用力一般可以很好地近似為彈性力。形象地講,若把原子比作小球的話,整個晶體猶如由許多規則排列的小球構成,而小球之間又彼此由彈簧連接起來一般,從而每個原子的振動都要牽動周圍的原子,使振動以彈性波的形式在晶體中傳播。這種振動在理論上可以認為是一系列基本的振動(即簡正振動)的疊加。當原子振動的振幅與原子間距的比值很小時(這在一般情況下總是固體中在定量上高度正確的原子運動圖象),如果我們在原子振動的勢能展開式中只取到平方項的話(這即所謂的簡諧近似),那麼,這些組成晶體中彈性波的各個基本的簡正振動就是彼此獨立的。換句話說,每一種簡正振動模式實際上就是一種具有特定的頻率ν、波長λ和一定傳播方向的彈性波,整個系統也就相當於由一系列相互獨立的諧振子構成。在經典理論中,這些諧振子的能量將是連續的,但按照量子力學,它們的能量則必須是量子化的,只能取hν的整數倍,即(其中為零點能)。這樣,相應的能態E就可以認為是由n個能量為hν的“激發量子”相加而成。而這種量子化了的彈性波的最小單位就叫聲子。
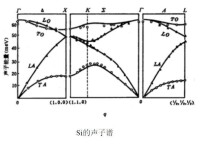
聲子譜實例
![聲子[物理名詞]](https://i1.twwiki.net/cover/w200/m0/1/m01a9b8539533c878ef24ef5214d8e3ca.jpg)
聲子[物理名詞]
因此,聲子用來描述晶格的簡諧振動,是固體理論中很重要的一個概念。按照量子力學,物體是由大量的原子構成,每種原子又都含有原子核和電子,因此固體內存在原子核之間的相互作用、電子間的相互作用還有原子核與電子間的相互作用。電子的運動規律可以用密度泛函理論得到,那麼原子核的運動規律就用聲子來描述。當然這兩個理論(密度泛函和聲子)都是近似的,因為解析的嚴格解到目前為止還沒有得到。而要嚴格地按照多體理論來描述這麼大量的原子和電子組成的系統,無論解析還是數值模擬都是一個未知數。
聲子是簡諧近似下的產物,如果振動太劇烈,超過小振動的範圍,那麼晶格振動就要用非簡諧振動理論描述。
聲子並不是一個真正的粒子,聲子可以產生和消滅,有相互作用的聲子數不守恆,聲子動量的守恆律也不同於一般的粒子,並且聲子不能脫離固體存在。聲子只是格波激發的量子,在多體理論中稱為集體振蕩的元激發或准粒子。
聲子的化學勢為零,屬於玻色子,服從玻色-愛因斯坦統計。聲子本身並不具有物理動量,但是攜帶有準動量,並具有能量。

聲子晶體
類似於光子在光子晶體中的傳播,彈性波在聲子晶體中傳播時,受其內部周期結構的作用,形成特殊的色散關係(能帶結構),色散關係曲線之間的頻率範圍稱為帶隙。
理論上,帶隙頻率範圍的彈性波傳播被抑制,而其它頻率範圍(通帶)的彈性波將在色散關係的作用下無損耗地傳播。當聲子晶體的周期結構存在缺陷時,帶隙頻率範圍內的彈性波將被局限在缺陷處,或沿缺陷傳播。因此,聲子晶體可用於控制彈性波的傳播,在新型聲學器件、減振降噪領域具有廣闊的應用前景。
在聲子晶體中,與彈性波傳播相關的密度和彈性常數不同的材料按結構周期性複合在一起,分佈在格點上相互不連通的材料稱為散射體,連通為一體的背景介質材料稱為基體。聲子晶體按其周期結構的維數可分為一維、二維和三維.
理想的聲子晶體模型一般認為在非周期方向上具有無限尺寸,這種假設只有在波長遠小於非周期方向尺寸時才合理。由於固體中彈性波傳播速度較快,實際工程中廣泛應用的梁、板等結構均不能滿足這一條件,因此,研究非周期方向上為有限尺寸的周期結構更有實際意義。為了區別於一維、二維理想聲子晶體,可將這類周期結構稱為聲子晶體結構。研究表明,聲子晶體梁板類結構同樣具有帶隙特性。
英文名稱:Acoustic Emission,AE
中文名稱:聲子發射
日文名稱:(えいい一),アコースティックエミッション
說明:在材料裂紋的端部,隨裂紋的擴展,會發射出各種頻率的彈性波,它被稱之為聲(子)發射。用壓電變換元件檢測此時發出的彈性波,可測定有無裂紋以及斷裂的開始,斷裂源的位置等。
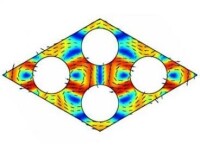
計算機模擬的聲子
當晶體中的載流子運動時,即會遭受到熱振動原子的散射(靜止原子並不散射載流子),它們交換能量將以ħωq為單元進行,若電子從晶格振動獲得ħωq能量,就稱為吸收一個聲子;若電子交給晶格ħωq能量,就稱為發射一個聲子。這種作用可採用載流子與聲子的散射來描述,即稱為 聲子散射。
系統中聲子的數目與溫度有關:因為溫度越高,晶格振動就越劇烈,其能量量子數目就越多,即聲子數也就越多。因此隨著溫度的上升,聲子散射載流子的作用也就越顯著。
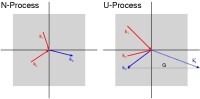
聲子散射過程
如果聲子的動量發生了變化,正如右圖的U-Process所示:
其中,G是反格子向量,值為;K1和K2兩個聲子碰撞所產生的第三聲子的動量已經超越了第一布里淵區(圖中的灰色方框代表了第一布里淵區的範圍)。第一布里淵區里包含著所有可能單獨存在的聲子的波向量的可能值。但是在這個過程中,能量是守恆的,也就是說。這種聲子散射機制隨著溫度的升高而不斷加強,也這是導致硅材料熱導率從25K時的5500W/m·K下降到300K時148W/m·K的主要原因。
除了三聲子散射過程之外,還存在著雜質散射和邊界散射,都會影響材料的熱導率。
當聲波(縱波)在晶體中傳播時,將造成晶體原子密度發生波動式的疏密變化——疏密波,並從而在晶體中產生額外的周期性勢場波(該勢場波的周期與聲波相同)。在Si、Ge等原子半導體中,聲波所產生的勢場波就是畸變勢周期性勢場(這種勢場波的波幅較小);而在壓電半導體中,聲波所產生的勢場波就是壓電周期性電勢場(這種勢場波的波幅很大)。因為在晶體中的聲波實際上與晶格振動的長聲學波在本質上是相同的,因此也可以把聲波量子化為聲子(晶格振動的能量子可以稱為是“熱聲子”)。從而聲波在晶體中所產生的勢場波可以認為就是聲子的作用效果——聲子勢場波。在晶體中存在聲子勢場波時,如果晶體電子的平均自由程比聲波的波長(λ=2π/q)要小(q為聲子的波數),則電子會不斷遭受聲子散射而損失能量,從而電子將被聲子勢場波的波谷所俘獲。在電子被聲子勢場波俘獲的情況下,當聲波在晶體中傳播時,電子即被聲子勢場波牽引著向前,這就是所謂聲子曳引效應。如圖所示。由於聲子勢場波的波幅越大,聲子曳引的作用也就越強,所以在壓電半導體中的聲子曳引效應較顯著。同時,超聲波也可以產生幅度較大的周期勢場波,所以超聲波牽引電子的作用也較強。
![聲子[物理名詞]](https://i1.twwiki.net/cover/w200/mb/4/mb4f9081ffcd1e7ea5534ca48e69fdd56.jpg)
聲子[物理名詞]
