靜電場
電荷周圍空間存在的特殊物質
靜電場,指的是觀察者與電荷相對靜止時所觀察到的電場。它是電荷周圍空間存在的一種特殊形態的物質,其基本特徵是對置於其中的靜止電荷有力的作用。庫侖定律描述了這個力。
根據靜電場的高斯定理:

靜電場
從安培環路定理來說它是一個無旋場.
根據環量定理,靜電場中環量恆等於零,表明靜電場中沿任意閉合路徑移動電荷,電場力所做的功都為零,因此靜電場是保守場.
根據庫侖定律,兩個點電荷之間的作用力跟它們的電荷量的乘積成正比,和它們距離的平方成反比,作用力的方向在它們的連線上,即,其中為兩電荷的電荷量(不計正負性)、k為靜電力常量,約為,r為兩電荷中心點連線的距離。注意,點電荷是不考慮其尺寸、形狀和電荷分佈情況的帶電體。是實際帶電體的理想化模型。當帶電體的距離比它們的大小大得多時,帶電體的形狀和大小可以忽略不計的點電荷。
一個帶電的物體靠近另一個導體時,兩個導體的電荷分佈發生明顯的變化,物理學中把這種現象叫做靜電感應。
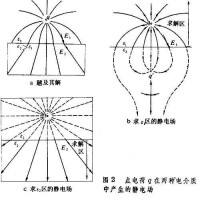
靜電場
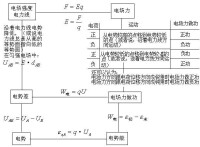
靜電場知識結構圖
式中P為電介質的極化強度,則可得高斯通量定理
式中q僅為S面內所有自由電荷,而不包括電介質的束縛電荷。高斯通量定理的微分形式為電位移的散度等於該點自由電荷(體)密度ρ,
電介質的極化強度P與電場強度E有關,而電通量密度又與P和E有關,故可得表示電介質的本構方程
由於靜電場是無旋場,故可用標量電位φ表徵靜電場(見電位)。電位與電場強度的關係是
式中Q點為電位參考點,可選在無窮遠處;P點為觀察點。上式的微分形式為電場強度等於電位的負梯度,即
在ε為常數的區域,
式中可記作,在直角坐標中
分別為一階與二階微分算符。這樣,可得電位φ所滿足的微分方程
稱為泊松方程。如果觀察點處自由電荷密度ρ為0,則
稱為拉普拉斯方程。泊松方程和拉普拉斯方程描述了靜電場空間分佈的規律性。可以證明,當已知ρ、ε及邊界條件時,泊松方程或拉普拉斯方程的解是惟一的,可以設法求解電位φ,再求出場中各處的E。
