統計假設

統計分佈就是形成總體中各個單位在各組間的分佈。其實質是把總體的全部單位按某標誌所分的組進行分配所形成的數列，所以又稱分配數列或分佈數列。統計分佈由兩個構成要素所組成：總體按某標誌所分的組，各組所佔有的單位數—次數。根據分組標誌的不同，分配數列分為品質分配數列和變數分配數列。由上面的概念，統計分佈包括兩個要素：總體按某標誌所分的組和各組的單位數(簡稱次數)。

根據分組標誌的不同，分配數列可分為品質分配數列和變數分配數列。按品質標誌分組所編成的分配數列叫做品質分配數列，簡稱品質數列；按數量標誌分組所編成的分配數列叫作分配數列，簡稱變數數列。

為研究問題的需要，預先設定的一種假設。在假設檢驗中，統計假設有原假設H0和備擇假設H1。例如，欲研究性別對學習成績的影響問題。定義Xi，Yi分別是男生、女生某學科成績，可設立原假設X=Y，通過統計方法進行推斷。

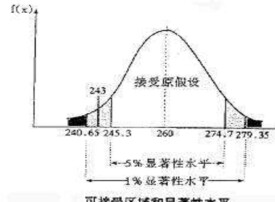
假設檢驗(Hypothesis Testing)是數理統計學中根據一定假設條件由樣本推斷總體的一種方法。具體作法是：根據問題的需要對所研究的總體作某種假設，記作H0；選取合適的統計量，這個統計量的選取要使得在假設H0成立時，其分佈為已知；由實測的樣本，計算出統計量的值，並根據預先給定的顯著性水平進行檢驗，作出拒絕或接受假設H0的判斷。常用的假設檢驗方法有u—檢驗法、t檢驗法、χ2檢驗法(卡方檢驗)、F—檢驗法，秩和檢驗等。

假設檢驗是抽樣推斷中的一項重要內容。它是根據原資料作出一個總體指標是否等於某一個數值，某一隨機變數是否服從某種概率分佈的假設，然後利用樣本資料採用一定的統計方法計算出有關檢驗的統計量，依據一定的概率原則，以較小的風險來判斷估計數值與總體數值(或者估計分佈與實際分佈)是否存在顯著差異，是否應當接受原假設選擇的一種檢驗方法。

用樣本指標估計總體指標，其結論有的完全可靠，有的只有不同程度的可靠性，需要進一步加以檢驗和證實。通過檢驗，對樣本指標與假設的總體指標之間是否存在差別作出判斷，是否接受原假設。這裡必須明確，進行檢驗的目的不是懷疑樣本指標本身是否計算正確，而是為了分析樣本指標和總體指標之間是否存在顯著差異。從這個意義上，假設檢驗又稱為顯著性檢驗。

假設檢驗的思想和方法的根據是小概率原理，具體地說當我們對問題提出原假設和備擇假設，並要檢驗“。是否可信時，可以先假設原假設是正確的，在此假定下，經過一次抽樣，若發生了一個小概率事件，可以根據“小概率事件在一次實驗中幾乎不可能發生”的理由，懷疑原假設原假設不真，而作出拒絕原假設的決定，反之，如果小概率事件沒有發生，就沒有理由拒絕襯原假設，從而接受原假設。

由於抽樣的隨機性，利用小概率原理對原假設是否成立作出判斷時，難免要犯兩類錯誤。邱芳對該問題進行相關研究，結論如下：

（1）犯兩類錯誤的概率是相互有關聯的，當樣本容量M固定時，犯第一類錯誤的概率的減小會導致犯另一類錯誤的增加。

（2）犯第一類錯誤的概率可以通過適當改變檢驗的拒絕域來進行調整。

（3）當樣本容量。給定時，由於很難得到第二類錯誤的表達式，在實際應用中，一般只是對犯第一類錯誤的概率加以控娜，特別是在進行單側檢驗時，最好把原假設取為預想的結果的反面。

（4）當零假設不真時，參數的真值越接近零假設下的值時，犯第二類錯誤的概率就越大。

（5）要同時降低犯兩類錯誤的概率，需要增加樣本容量。