.極限集
.極限集
極限集(limit set)是動力系統由極限點組成的集合。極限點指隨著時間向正負兩個方向趨於無窮時該點所在的軌道會無窮次接近它的點。如果只考慮時間趨於正或負無窮,則可分別得到ω極限集或α極限集。極限集是動力系統研究的基本對象。軌道的極限集是不變閉集,如果相空間是緊的,極限集也總存在。不動點和周期軌都是極限集的例子。根據龐卡萊-班狄克遜(Poincaré-Bendixson)定理,平面向量場的極限集通常由有限條軌道與平衡點連接而成。空間系統的極限集有時很複雜,如奇怪吸引子。
如果存在趨∞於的時間序列 使得 收斂於,則稱 是軌線 或點 的 極限點。這表明當 趨向於 時,無數次地靠近,所有 極限點的集合稱為是極限集,記作。
類似地,如果存在趨於 的時間序列 使得 收斂於,則稱 是軌線 或點 的極限點,所有 極限點的集合稱為 極限集,記作。
設 是一條軌線,則下面 極限集的性質成立:
(i) 極限集只依賴於軌線而不依賴於特定點,因此對任意的t,有;
(ii) 是不變集:若,那麼對所有的正t或負t,軌線 都屬於;
(iii) 是閉集(即 包含它所有的極限點);
(iv) 若,則有;
另外,若 對 是有界的(即存在常數C使得,則下面的(v)和(vi)也成立:
(v) 非空;
(vi) 是連通的,即它不能由多塊區域組成。
若 對 是有界的,則 極限集有類似的性質。
性質(i)可直接由 極限集的定義推出。
性質(ii)可由流的連續性得到。
若 中的序列 收斂於,而 是 的極限點,這兩點相結合可推出性質(iii)。
由性質(ii)和(iii)可推出性質(iv)。
性質(v)成立是因為軌線要不斷地回到相空間中的某處。
性質(vi)成立是因為軌線本身是連通的。
極限集還可以表示為軌線上時間大於 的部分的閉包對所有 求交集,即
例1 考慮方程組
引入極坐標后可以很容易地理解該方程組,極坐標r滿足,兩邊關於t進行微分並結合方程的表達式可得
或
同理,取角變數 滿足,兩邊關於t進行微分,則有
於是
因此,解沿逆時針方向、以相同的角速度繞原點旋轉,關於r的方程有一個吸引的不動點r=1和一個排斥的不動點r=0.從而在平面坐標下的方程有一個半徑為1的圓形周期軌道,和一個排斥的不動點——原點,參見圖1(a)
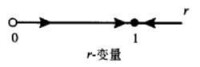
圖1(a)
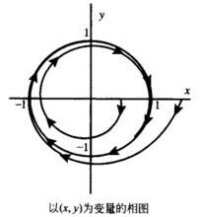
圖1(b)
從單位圓外出發的軌線 都趨向於該單位圓,而不是趨於圓上的某個點,但對於圓上任一點z,每經過 單位的時間后更接近於z,因此存在時間序列 使得 收斂於z.顯然所取的z不同得到的 也不同,鑒於只考慮t趨向於無窮的情況,所有這些點所成之集稱為極限集,這種記法考慮到了 是希臘字母表的最後一個字母。同理,t趨向負無窮時軌線的極限點集稱為是極限集。