韋布爾分佈
1951年韋布爾提出的概率分佈
韋布爾分佈,即韋伯分佈(Weibull distribution),又稱韋氏分佈或威布爾分佈,是可靠性分析和壽命檢驗的理論基礎。
威布爾分佈在可靠性工程中被廣泛應用,尤其適用於機電類產品的磨損累計失效的分佈形式。由於它可以利用概率值很容易地推斷出它的分佈參數,被廣泛應用於各種壽命試驗的數據處理。
(History)
1.1927年,Fréchet(1927)首先給出這一分佈的定義。
2.1933年,Rosin和Rammler在研究碎末的分佈時,第一次應用了韋伯分佈(Rosin,P;Rammler,E.(1933),"The Laws Governing the Fineness of Powdered Coal",Journal of the Institute of Fuel 7:29-36.)。
3.1951年,瑞典工程師、數學家Waloddi Weibull(1887-1979)詳細解釋了這一分佈,於是,該分佈便以他的名字命名為Weibull Distribution。
韋布爾分佈
(Properties)
均值(mean)
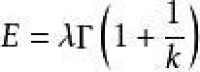
韋布爾分佈
方差(variance)
韋布爾分佈
韋布爾分佈
韋布爾分佈
工業製造
研究生產過程和運輸時間關係。
極值理論
預測天氣
可靠性和失效分析
雷達系統
對接受到的雜波信號的依分佈建模。
擬合度
無線通信技術中,相對指數衰減頻道模型,Weibull衰減模型對衰減頻道建模有較好的擬合度。
量化壽險模型的重複索賠
預測技術變革
風速
由於曲線形狀與現實狀況很匹配,被用來描述風速的分佈。
