餘切
餘切
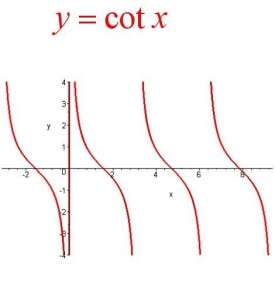
在在直角三角形中,某銳角的相鄰直角邊和相對直角邊的比,叫做該銳角的餘切。餘切與正切互為倒數,用“cot+角度”表示。餘切函數的圖象由一些隔離的分支組成(如圖)。餘切函數是無界函數,可取一切實數值,也是奇函數和周期函數,其最小正周期是π 。
任意角終邊上除頂點外的任一點的橫坐標除以該點的非零縱坐標,角的頂點與平面直角坐標系的原點重合,而該角的始邊則與正x軸重合。簡單點理解:直角三角形任意一銳角的鄰邊和對邊的比,叫做該銳角的餘切。
餘切表示時用“cot+角度”,如:30°的餘切表示為cot30°;角A的餘切表示為cotA。舊用ctgA來表示餘切,和cotA是一樣的。假設∠A的對邊為a、鄰邊為b,那麼:cot A= (即鄰邊比對邊)。
然後由泰勒級數得出
“餘切序列”是蝴蝶效應的一個典型例子。以下三個數列每一項都是前一項的餘切;初值分別為1、1.00001、1.0001,但是從第10項開始,三個數列開始形成巨大的分歧。這就是混沌的數列,經過足夠多項后,得到的數字完全可以看作是隨機的,混沌的。
| a[n+1]=cot(a[n]) | ||
| 甲 | 乙 | 丙 |
| 1 | 1.00001 | 1.0001 |
| 0.642092616 | 0.642078493 | 0.641951397 |
| 1.337253178 | 1.337292556 | 1.337647006 |
| 0.237883877 | 0.237842271 | 0.237467801 |
| 4.124136332 | 4.124885729 | 4.131642109 |
| 0.667027903 | 0.66594562 | 0.656236434 |
| 1.269957474 | 1.272789148 | 1.29854625 |
| 0.310255611 | 0.30715408 | 0.279182071 |
| 3.119060463 | 3.152660499 | 3.488344037 |
| -44.37343796 | 90.34813006 | 2.767389601 |
| -2.424894313 | -1.056234059 | -2.546431398 |
| 1.147785023 | -0.565363802 | 1.476981164 |
| 0.45018926 | -1.576175916 | 0.094091367 |
| 2.069157407 | 0.005379641 | 10.5965853 |
| -0.544176342 | 185.8842166 | 0.421601998 |
| -1.652562399 | 1.705748261 | 2.229677257 |
| 0.081948782 | -0.135777195 | -0.774313338 |
| 12.17541547 | -7.31969225 | -1.02241908 |
| -2.42617226 | -0.59169349 | -0.610874688 |
| 1.150750903 | -1.48807061 | -1.428119284 |
| 0.44662703 | -0.082914948 | -0.143653138 |
| 2.088110796 | -12.03290058 | -6.913261967 |
| -0.569001376 | 1.693228262 | -1.371305422 |
敘利亞天文學家、數學家阿爾巴坦尼(850-929)於920年左右,製成了自0到90度相隔1度的餘切表。
14世紀中葉,成吉思汗的後裔,中亞細亞的阿魯伯(1393--1449)組織了大規模的天文觀測和數學用表的計算,他的正弦表精確到小數9位,他還製作了30到45度之間相隔為1",45到90度的相隔為5"7'的正切表。
英國數學家、坎特伯雷大主教布拉瓦丁(1290-1349)首先把正切、餘切引入他的三角計算之中。
餘切函數的函數圖像如圖2所示,其主要性質如下: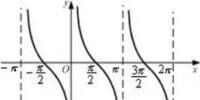

餘切
(1)定義域:餘切函數的定義域是;
(2)值域:餘切函數的值域是實數集R,沒有最大值、最小值;
(3)周期性:餘切函數是周期函數,周期是;
(4)奇偶性:餘切函數是奇函數,它的圖像關於原點對稱;
(5)單調性:餘切函數在每一個開區間上都是減函數。