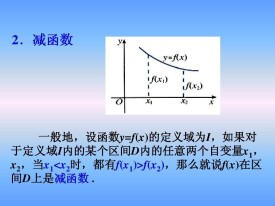
減函數
減函數
函數f(x)的定義域為I,如果對於定義域I內的某個區間D上的任意兩個自變數的值x1,x2,當x1f(x2),那麼就說f(x)在這個區間上是減函數,並稱區間D為遞減區間。減函數的圖像從左往右是下降的,即函數值隨自變數的增大而減小。判斷一個函數是否為減函數可以通過定義法、圖像法、直觀法或利用該區間內導數值的正負來判斷。
一般地,設函數的定義域為,如果對於定義域I內的某個區間上的任意兩個自變數的值,當時,都有,那麼就說在區間上是減函數。即隨著自變數增大,函數值減小的函數為減函數。
如果函數在區間上是增函數或減函數,那麼就或函數在這一區間具有(嚴格的)單調性,區間就叫做函數的單調區間。
用定義法證明單調性的步驟:
(1)任取,且滿足;
(2)作差;
(3)變形(通常是因式分解和配方);
(4)定號(即判斷的正負);
(5)下結論(指出函數f(x)在給定的區間D上的單調性)。
在證明函數為減函數時,只需要證明:當時。在減函數的圖像中,函數圖像從左往右是下降的,即函數值隨自變數的增大而減小。
(1)定義法:即“取值(定義域內)→作差→變形→定號→判斷”;
(2)圖像法:先作出函數圖像,利用圖像直觀判斷函數的單調性;
(4)求導法:假定函數在區間上連續且在上可微,若每個點有,則在上是遞增的;若每個點有,則在上是遞減的。
(1)函數的單調性是對函數定義域內的某個子區間而言的,是函數的局部性質;
(2)函數在給定區間上的單調性是函數在該區間上的整體性質;
(3)函數的單調性定義中有三個特徵:任意性、有大小、屬於同一個單調區間;
(4)求函數的單調區間,必須先求定義域。
(5)區間端點的寫法:對於單獨的一點,由於它的函數值是唯一確定的常數,沒有增減變化,所以不存在單調性問題,因此在寫單調區間時,可以包括端點,也可以不包括端點,但對於某些點無意義時,單調區間就不包括這些點。
(1)增函數+增函數=增函數;
(2)減函數+減函數=減函數;
(3)增函數-減函數=增函數;
(4)減函數-增函數=減函數。
判斷函數的單調性。
解:易得該函數是整函數,故定義域為R。
(1)利用定義法來判斷該函數的單調性。
任取,且滿足,則有:
最終兩個因式中第一個因式小於零,第二個因式恆大於零,且兩因式前有一個負號,故有,即有:當時,有,故該函數在R上為減函數。
(2)利用圖像法來判斷。
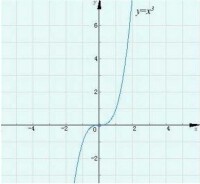
y=x^3的圖像
(3)利用求導法來判斷。
對函數進行求導,得恆成立,故有該函數在定義域R上為減函數。