反比例函數
反比例函數
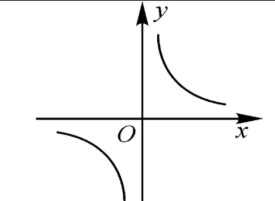
反比例函數的圖像屬於以原點為對稱中心的中心對稱的雙曲線（hyperbola）,反比例函數圖象中每一象限的每一條曲線會無限接近X軸Y軸但不會與坐標軸相交（y≠0）。
一般地，如果兩個變數x、y之間的關係可以表示成y=k/x (k為常數，k≠0)的形式，那麼稱y是x的反比例函數。因為y=k/x是一個分式，所以自變數X的取值範圍是X≠0。而y=k/x有時也被寫成xy=k或y=k·x^（-1）。表達式為：x是自變數，y是因變數，y是x的函數。
一般的，如果兩個變數x，y之間的關係可以表示成 (k為常數，k≠0，x≠0），其中k叫做反比例係數，x是自變數，y是x的函數，x的取值範圍是不等於0的一切實數，且y也不能等於0。k>0時，圖象在一、三象限。k<0時，圖象在二、四象限。k的絕對值表示的是x與y的坐標形成的矩形的面積。
x是自變數，y是因變數，y是x的函數
（即：y=kx^-1）
(k為常數且k≠0，x≠0）
若此時比例係數為：
自變數的取值範圍
① 在一般的情況下 , 自變數 x 的取值範圍可以是不等於0的任意實數。
② 函數 y 的取值範圍也是任意非零實數。
解析式
其中x是自變數，y是x的函數，其定義域是不等於0的一切實數，
即 {x|x≠0,x屬於R這個範圍。R是實數範圍。也就是x是實數}。
下面是一些常見的形式：y*x=-1,y=x^(-1)*k（k為常數(k≠0），x不等於0）
當k>0時，兩支曲線分別位於第一、三象限內；當k<0時，兩支曲線分別位於第二、四象限內，兩個分支無限接近x和y軸，但永遠不會與x軸和y軸相交.
圖象畫法
1）列表
| x | ... | -3 | -2 | -1 | 1 | 2 | 3 | 4 | ... |
| y | ... | -4 | -6 | -12 | 12 | 6 | 4 | 3 | ... |
2）在平面直角坐標系中標出點。
3）用平滑的曲線連接點。
1.當K>0時，在圖象所在的每一象限內，Y隨X的增大而減小。
2.當K<0時，在圖象所在的每一象限內，Y隨X的增大而增大。
當兩個數相等時那麼曲線呈彎月型。
k的意義及應用
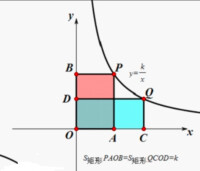
過反比例函數（ ）圖象上任意一點P（x,y），作兩坐標軸的垂線，兩垂足、原點、P點組成一個矩形，矩形的面積為。過反比例函數圖象一點，作任一坐標軸的垂線，並連接原點，圍成的三角形的面積為。
研究函數問題要透視函數的本質特徵。反比例函數中，比例係數k有一個很重要的幾何意義，那就是：過反比例函數圖象上任一點P作x軸、y軸的垂線PM、PN，垂足為M、N則矩形PMON的面積為。
所以，對雙曲線上任意一點作x軸、y軸的垂線，它們與x軸、y軸所圍成的矩形面積為常數。這個常數是k的絕對值。在解有關反比例函數的問題時，若能靈活運用反比例函數中k的幾何意義，會給解題帶來很多方便。
合併圖冊
當k>0時，圖象分別位於第一、三象限，每一個象限內，從左往右，y隨x的增大而減小；
當k<0時，圖象分別位於第二、四象限，每一個象限內，從左往右，y隨x的增大而增大。
k>0時，函數在x<0上同為減函數、在x>0上同為減函數；k<0時，函數在x<0上為增函數、在x>0上同為增函數。
因為在 (k≠0)中，x不能為0，y也不能為0，所以反比例函數的圖象不可能與x軸相交，也不可能與y軸相交，只能無限接近x軸，y軸。
在一個反比例函數圖像上任取兩點，過點分別作x軸，y軸的平行線，與坐標軸圍成的矩形面積為|k|，
反比例函數上一點 向x 、y 軸分別作垂線，分別交於y軸和x軸，則QOWM的面積為|k|，則連接該矩形的對角線即連接OM,則RT△OMQ的面積=½|k|。
反比例函數圖象不與x軸和y軸相交的漸近線為：x軸與y軸。
k值相等的反比例函數圖象重合，k值不相等的反比例函數圖象永不相交。
|k|越大，反比例函數的圖象離坐標軸的距離越遠。
反比例函數圖象是中心對稱圖形，對稱中心是原點；反比例函數的圖象也是軸對稱圖形，其對稱軸為 y=x或y=-x；反比例函數圖象上的點關於坐標原點對稱。
反比例函數
反比例函數關於正比例函數y=±x軸對稱，並且關於原點中心對稱。
反比例函數圖象上有一點P（m, n）其坐標是關於t的一元二次方程 t^2+3t+k=0的兩根，且P到原點的距離為根號13，求該反比例函數的解析式．
分析：
要求反比例函數解析式，就是要求出k，為此我們就需要列出一個關於k的方程．
解：∵ m, n是關於t的方程 的兩根
∴ m+n=-3，mn=k,
又∵P到原點的距離為根號13
m＾2+n＾2=13, m+n=-3;
∴ (m+n)＾2-2mn=13, m+n=-3；
∴ 9-2k=13
∴ k=-2
∴該反比例函數的解析式為y=-2/x.
直線與位於第二象限的雙曲線 相交於A、A1兩點，過其中一點A向x、y軸作垂線，垂足分別為B、C，矩形ABOC的面積為6，求：
（1）求雙曲線的解析式
分析：矩形aboc的邊AB和AC分別是A點到x軸和y軸的垂線段，設A點坐標為（m,n），則AB=|n|, AC=|m|，
根據矩形的面積公式知|m·n|=6.
由已知條件知，該雙曲線位於第二、四象限，因此，A點坐標值異號，
即雙曲線的解析式為xy=-6.例3
已知一次函數y=-x+6和反比例函數 y=x/k（k≠0）
（2）k滿足什麼條件時，這兩個函數在同一坐標系中的圖像有兩個交點？
（3）當圖像有兩個交點時（設為A和B），判斷∠AOB是銳角、鈍角還是直角？說明理由。解（1）一次函數y=-x+6和反比例函數y=x/k（k不等於零）有兩個交點，即
化簡的有兩個交點 則方程有兩個不同的解
即所以k<9且k不等於0
（2）當0
已知函數.
（1）當m為何值時，y是x的正比例函數?
（2）當m為何值時，y是x 的反比例函數？
解（1）正比例函數則x次數是1
(m-2)(m+1)=0
m=2,m=-1
係數不等於0
m-1≠0
所以m=2,m=-1
（2）反比例函數則x次數是-1
m(m-1)=0
m=0,m=1
係數不等於0
m-1≠0
所以捨去m=1
因此m=0
一矩形的面積為24，則該矩形的長x cm與寬y cm之間的關係是什麼？請寫出函數表達式，若要求矩形的各邊長均為整數，請畫出所有可能的的矩形。
解 面積xy=24
函數表達式(x>0)
矩形的各邊長均為整數
可以取x=1，2，3，4，6，8，12，24
形如 (k為常數且k≠0)的函數，叫做反比例函數。
自變數x的取值範圍是不等於0的一切實數。
反比例函數圖象性質：反比例函數的圖象為雙曲線。
由於反比例函數屬於奇函數，有對稱中心，圖象關於原點對稱。
另外，從反比例函數的解析式可以得出，在反比例函數的圖象上任取一點，向兩個坐標軸作垂線，這點、兩個垂足及原點所圍成的矩形面積是定值，為∣k∣。
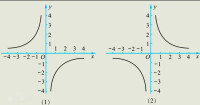
如圖，上面給出了k分別為正和負（2和-2）時的函數圖象。
當K>0時，反比例函數圖象經過一，三象限，是減函數
當K<0時，反比例函數圖象經過二，四象限，是增函數
反比例函數圖象只能無限趨向於坐標軸，無法和坐標軸相交。
1.過反比例函數圖象上任意一點作兩坐標軸的垂線段，這兩條垂線段與坐標軸圍成的矩形的面積為|k|。
2.對於雙曲線，若在分母上加減任意一個實數m(m為常數)，就相當於將雙曲線圖象向左或右平移m個單位。（加一個數時向左平移，減一個數時向右平移）
設n為正整數，則n的所有取值所對應的函數 交於（1，1）和（-1，-1），且當n越大並且x>1時，,圖像離坐標軸近；當n越大並且0x時，圖像離坐標軸近。
基本信息
- 中文名
- 反比例函數
- 外文名
- inverse proportional function
- 計算公式
- y=k/x，其中k∈(-∞,0)∪(0,+∞)
- 圖像對稱性
- 軸對稱，中心對稱圖形
- 值域
- (-∞,0)∪(0,+∞)
- 定義域
- {x|x≠0}
- k小於0時
- 2、4象限
- 應用範圍
- 幾何、數學，計算機等
- k大於0時
- 1、3象限
目錄