正定核是一類特殊的對稱核,其相應的線性積分運算元的特徵值都是正的。若 K 僅有有限多個負特徵值,則稱 k(x,y) 必是擬正定核。
正定核是一類特殊的對稱核,其相應的線性積分運算元的特徵值都是正的。
設對稱核 k(x,y) 是 上的平方可積函數, K 是以 k(x,y) 為核的線性積分運算元。如果 K 作為映 入 的運算元,其所有的
特徵值都是正的,則稱 k(x,y) 是正定核。
若 K 僅有有限多個負特徵值,則稱 k(x,y) 必是擬正定核。
(kernel)
核是
位勢論的基本概念。在位勢論中,所謂核,常指一般位勢的核。
若 恆成立,則稱 K 為正核;令(K' 稱為 K 的
轉置核),若 K'=K,則稱 K 為對稱核;當Ω 為
阿貝爾群且有 時,則稱 K 為平移不變核;若對於任意有緊支集的 μ ,有
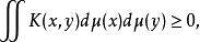
正定核
則稱 K 為正定核,此外,還有各種廣義形式的核,如
測度核、廣義函數核等。