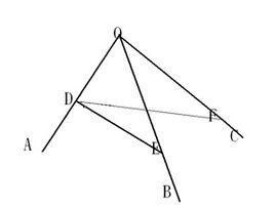
三面角餘弦定理
三面角餘弦定理
在三面角O-ABC中，設二面角B-OA-C為∠OA，則有：
cosBOC=cosAOBcosAOC+sinAOBsinAOCcosOA
或
cosOA=(cosBOC-cosAOBcosAOC)/sinAOBsinAOC
文字敘述為：三面角中任一二面角的餘弦值，等於其所對面角的餘弦減去另兩個面角的餘弦之積，再除以這兩個面角的正弦之積。
根據這個定理，結合三正弦定理就可以求直線和平面所成角或二面角。
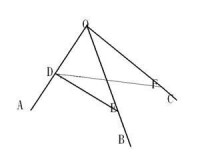
三面角餘弦定理
考慮有向線段 OD、 OE、 OF、 DE、 DF。易知：
；
則實際是要證明：
整理得
即是要證明；
顯然， ，
注意到，即可證明原式。
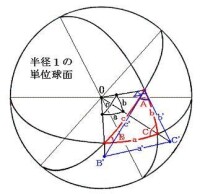
三面角餘弦定理
在中，由餘弦定理得
在△OB'C'中，由余弦定理得
∴
兩邊乘以得
移項，整理得
化簡得
也就是
在三面角中，設二面角為，則有：
將三面角O-ABC的頂點與單位球的球心重合，並設三邊與球面分別交於A、B、C。根據球面三角形的定義，在球面△ABC中，。則餘弦定理的第一形式可化為：
餘弦定理的第二形式可化為：
由於球面三角形與其極對稱三角形之間存在定量的邊角關係，因此不妨設球面△ABC的極對稱三角形為，則在中，由余弦定理的第一形式得
∵
∴上式可化為
即
證明完畢
三面角餘弦定理的全向量證明
基本信息
- 中文名
- 三面角餘弦定理
- 應用學科
- 數學
- 適用領域
- 求二面角
- 表達式
- cosBOC=cosAOBcosAOC+sinAOBsinAOCcosOA