貝葉斯分類器
分類錯誤概率最小的分類器
貝葉斯分類器是各種分類器中分類錯誤概率最小或者在預先給定代價的情況下平均風險最小的分類器。它的設計方法是一種最基本的統計分類方法。其分類原理是通過某對象的先驗概率,利用貝葉斯公式計算出其後驗概率,即該對象屬於某一類的概率,選擇具有最大后驗概率的類作為該對象所屬的類。
研究較多的貝葉斯分類器主要有四種,分別是Naive Bayes、TAN、BAN和GBN。
貝葉斯網路是一個帶有概率註釋的有向無環圖,圖中的每一個結點均表示一個隨機變數,圖中兩結點間若存在著一條弧,則表示這兩結點相對應的隨機變數是概率相依的,反之則說明這兩個隨機變數是條件獨立的。網路中任意一個結點X均有一個相應的條件概率表(Conditional Probability Table, CPT),用以表示結點X在其父結點取各可能值時的條件概率。若結點X無父結點,則X的CPT為其先驗概率分佈。貝葉斯網路的結構及各結點的CPT定義了網路中各變數的概率分佈。
貝葉斯分類器是用於分類的貝葉斯網路。該網路中應包含類結點C,其中C 的取值來自於類集合,還包含一組結點,表示用於分類的特徵。對於貝葉斯網路分類器,若某一待分類的樣本D,其分類特徵值為 ,則樣本D屬於類別c的概率應滿足下式:
而由貝葉斯公式:
其中可由領域專家的經驗得到,而和 的計算則較困難。
應用貝葉斯網路分類器進行分類主要分成兩階段。第一階段是貝葉斯網路分類器的學習,即從樣本數據中構造分類器,包括結構學習和CPT學習;第二階段是貝葉斯網路分類器的推理,即計算類結點的條件概率,對分類數據進行分類。這兩個階段的時間複雜性均取決於特徵值間的依賴程度,甚至可以是NP完全問題,因而在實際應用中,往往需要對貝葉斯網路分類器進行簡化。根據對特徵值間不同關聯程度的假設,可以得出各種貝葉斯分類器,Naive Bayes、TAN、BAN、GBN就是其中較典型、研究較深入的貝葉斯分類器。
在具有模式的完整統計知識條件下,按照貝葉斯決策理論進行設計的一種最優分類器。
最小錯誤概率貝葉斯分類器
貝葉斯分類器
貝葉斯分類器
進行計算
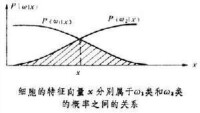
一般情況下,不能直接得到后驗概率而是要通過貝葉斯公式 進行計算。式中的為在模式屬於類的條件下出現x的概率密度,稱為x的類條件概率密度;為在所研究的識別問題中出現類的概率,又稱先驗概率;P(x)是特徵向量x的概率密度。分類器在比較后驗概率時,對於確定的輸入x,P(x)是常數,因此在實際應用中,通常不是直接用后驗概率作為分類器的判決函數(見線性判別函數)而採用下面兩種形式:
對所有的c個類計算。與中最大值相對應的類別就是x的所屬類別。
最小風險貝葉斯分類器
由於客觀事物的複雜性,分類器作出各種判決時的風險是不一樣的。例如將癌細胞誤判為正常細胞的風險就比將正常細胞誤判為癌細胞的風險大。因此,在貝葉斯分類器中引入了風險的概念。在實際應用中根據具體情況決定各種風險的大小,通常用一組係數來表示。表示分類器將把識別樣本分類為,而該樣本的真正類別為時的風險。設計最小風險分類器的基本思想是用后驗概率計算將x分類為的條件風險比較各的大小,與最小值對應的類別是分類的結果。評價這種分類器的標準是平均風險,它的平均風險最小。在實際應用時,后驗概率是難以獲得的,根據模式類別的多少和的取值方式,可設計出各種分類器,例如模式為兩類時,判別函數為如果選擇和為零,和為1,它就是兩類最小錯誤概率分類器。實際上,最小錯誤概率分類器是最小風險分類器的一種特殊情況。