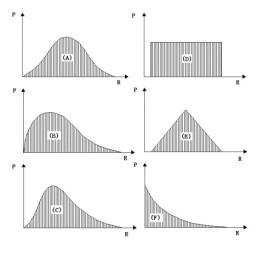
概率密度函數
描述隨機變數的輸出值
概率密度函數是專業術語,拼音為gài lǜ mì dù hán shù,在數學中,連續型隨機變數的概率密度函數(在不至於混淆時可以簡稱為密度函數)是一個描述這個隨機變數的輸出值,在某個確定的取值點附近的可能性的函數。而隨機變數的取值落在某個區域之內的概率則為概率密度函數在這個區域上的積分。當概率密度函數存在的時候,累積分佈函數是概率密度函數的積分。概率密度函數一般以小寫標記。
連續型隨機變數的概率密度函數有如下性質:
如果概率密度函數在一點x上連續,那麼累積分佈函數可導,並且它的導數:由於隨機變數X的取值 只取決於概率密度函數的積分,所以概率密度函數在個別點上的取值並不會影響隨機變數的表現。更準確來說,如果一個函數和X的概率密度函數取值不同的點只有有限個、可數無限個或者相對於整個實數軸來說測度為0(是一個零測集),那麼這個函數也可以是X的概率密度函數。
連續型的隨機變數取值在任意一點的概率都是0。作為推論,連續型隨機變數在區間上取值的概率與這個區間是開區間還是閉區間無關。要注意的是,概率,但並不是不可能事件。
這裡指的是一維連續隨機變數,多維連續變數也類似。
隨機數據的概率密度函數:表示瞬時幅值落在某指定範圍內的概率,因此是幅值的函數。它隨所取範圍的幅值而變化。
密度函數f(x) 具有下列性質:
① ;
② ;
③
最簡單的概率密度函數是均勻分佈的密度函數。對於一個取值在區間[a,b]上的均勻分佈函數,它的概率密度函數:也就是說,當x不在區間[a,b]上的時候,函數值等於0;而在區間[a,b]上的時候,函數值等於這個函數。這個函數並不是完全的連續函數,但是是可積函數。
隨著參數μ和σ變化,概率分佈也產生變化。
對概率密度函數作傅里葉變換可得特徵函數。
特徵函數與概率密度函數有一對一的關係。因此知道一個分佈的特徵函數就等同於知道一個分佈的概率密度函數。
隨機變數X的n階矩是X的n次方的數學期望,即
X的方差為
更廣泛的說,設g為一個有界連續函數,那麼隨機變數g(X)的數學期望為: