最小阻力定律
物理領域定律
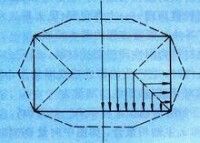
最短法線法則示意圖
1、最短法線法則。鐓粗矩形柱體時,在垂直鐓粗方向的任一剖面內的任一點,其移動方向朝著與周邊垂直的最短法線方向進行的(見圖)。
2、最小周邊法則。橫斷面為任意形狀的稜柱體或圓柱體,在存在摩擦的條件下進行塑性鐓粗時,將力圖使斷面的周界為最小,在極限情況下為一圓。
體積不變定律與最小阻力定律是怎麼形成的?
鋼錠在頭幾道軋制中因其縮孔、疏鬆、氣泡、裂紋等缺陷受壓縮而緻密,體積有所減小,此後各軋制道次的金屬體積就不再發生變化。這種軋制前後體積不變的客觀事實叫做體積不變定律。它是計算軋制變形前後的軋件尺寸的基本依據。舟后的軋件尺寸變化見圖2-23。
軋前的軋件體積以V1表示,軋后的軋件體積以V2表示。因為矩形體積等於軋件的高×寬×長,
所以V1= HBL (2-2)
V2 = hbl (2-3)
根據體積不變定律,軋件軋制前後體積相等,即
Vl = V2 (2-4)
HBL=hbl
所以
根據式2-4可以計算軋制前後乾件的尺寸變化。
