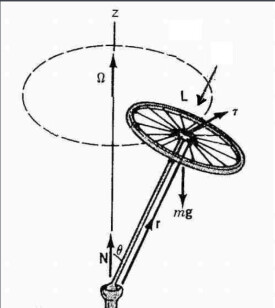
角動量守恆定律

當一個質點繞原點運動時，它的角動量L=RxP。這裡，R是質點相對於原點的位置向量；P是質點的線性動量；而x表示矢量積。

具有一定質量的物體繞一固定軸轉動，它的角動量L可表示為這個物體的慣性矩I和它的角速度向量w的乘積，即L=Ixw.

角動量又稱為動量矩，是一個矢量，是位矢叉乘於動量。

角動量守恆定律是物理學的普遍定律之一，反映質點和質點系圍繞一點或一軸運動的普遍規律；反映不受外力作用或所受諸外力對某定點（或定軸）的合力矩始終等於零的質點和質點系圍繞該點（或軸）運動的普遍規律。

例如一個在向心力場中運動的質點，始終受到一個通過力心的向心力作用，因向心力對力心的力矩為零，所以根據角動量定理，該質點對力心的角動量守恆。因此，質點軌跡是平面曲線，且質點對力心的矢徑在相等的時間內掃過相等的面積。如果把太陽看成力心，行星看成質點，則上述結論就是開普勒行星運動三定律之一，即開普勒第二定律。

一個不受外力或外界場作用的質點系，其質點之間相互作用的內力服從牛頓第三定律，因而質點系的內力對任一點的主矩為零，從而導出質點系的角動量守恆。如質點系受到的外力系對某一固定軸之矩的代數和為零，則質點系對該軸的角動量守恆。

角動量守恆定律是物理和自然界的一個重要定律，它在日常生活、天體物理、微觀物理和工程等許多方面都有廣泛的應用。例如：當滑冰者手臂收縮時，自我旋轉滑冰者的轉動速度就會加快。用角動量守恆定律也可解析中子星有很高的轉動速率等。另外，角動量守恆定律也是陀螺效應的原因。

角動量守恆定律反映了質點和質點系圍繞一點或一軸運動的普遍規律。如一質量為 m的質點受指向固定中心O的向心力F的作用，因力F對O點的力矩為零，根據牛頓第二定律可推得質點對O點的角動量守恆，Lo=r×mv=常矢量，此常矢量決定於運動的起始條件，r為質點對於O點的矢徑,v為質點的速度。如將太陽看成固定中心，行星看成質點，則角動量守恆表明行星軌道必在一平面上。矢徑在相等的時間內掃過的面積相等，這就是開普勒行星運動三定律之一—開普勒第二定律 。

角動量守恆也是微觀物理學中的重要基本規律。在基本粒子衰變、碰撞和轉變過程中都遵守反映自然界普遍規律的守恆定律，如能量守恆定律、動量守恆定律和角動量守恆定律等。1931 年，W.泡利根據守恆定律，推測自由中子衰變時有反中微子產生，1956年後這一結論為實驗所證實。