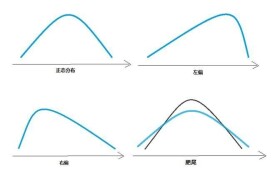
偏度

偏度(Skewness)亦稱偏態、偏態係數。表徵概率分佈密度曲線相對於平均值不對稱程度的特徵數。直觀看來就是密度函數曲線尾部的相對長度。

定義上偏度是樣本的三階標準化矩，定義式如下，其中分別表示二階和三階中心距：

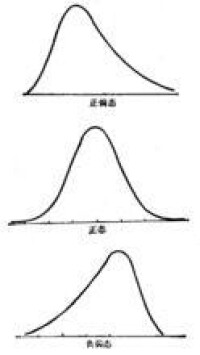
正態分佈的偏度為0，兩側尾部長度對稱。若以bs表示偏度。bs<0稱分佈具有負偏離，也稱左偏態，此時數據位於均值左邊的比位於右邊的少，直觀表現為左邊的尾部相對於與右邊的尾部要長，因為有少數變數值很小，使曲線左側尾部拖得很長；bs>0稱分佈具有正偏離，也稱右偏態，此時數據位於均值右邊的比位於左邊的少，直觀表現為右邊的尾部相對於與左邊的尾部要長，因為有少數變數值很大，使曲線右側尾部拖得很長；而bs接近0則可認為分佈是對稱的。若知道分佈有可能在偏度上偏離正態分佈時，可用偏離來檢驗分佈的正態性。右偏時一般算術平均數>中位數>眾數，左偏時相反，即眾數>中位數>平均數。正態分佈三者相等。

在實際計算中雖然可以採用定義式進行計算，但是需要多次遍歷各個樣本以計算均值和方差，當樣本容量很大時耗時很大。所以常常利用1至3階原點矩進行計算：

徠首先：

於是：

上面的矩方法同時還適用於峰度的計算。針對偏度還所以可以使用下面公式簡化計算：

對於n個樣本值的偏度，計算方法如下：

這裡 是第i個樣本，, 是樣本標準差. g1 是總體偏度的有偏估計。通常的偏度估計公式：

峰度（Kurtosis）與偏度類似，是描述總體中所有取值分佈形態陡緩程度的統計量。這個統計量需要與正態分佈相比較，峰度為0表示該總體數據分佈與正態分佈的陡緩程度相同；峰度大於0表示該總體數據分佈與正態分佈相比較為陡峭，為尖頂峰；峰度小於0表示該總體數據分佈與正態分佈相比較為平坦，為平頂峰。峰度的絕對值數值越大表示其分佈形態的陡緩程度與正態分佈的差異程度越大。

峰度的具體計算公式為：