光孤子
光孤子
自從1973年被Hasegawa和Tappert提出以後,引起了人們廣泛研究。空間光孤子是光束在傳播過程中由非線性效應平衡衍射效應的結果,空間光孤子一直是非線性光學研究前沿。光孤子在全光網路,光通信以及光邏輯器件方面有著非常重要的應用,在Snyder和Mitchell開創性地提出強非局域下空間光孤子模型后,有關強非局域非線性介質中的孤子研究在近幾年一直是熱點。Guo等在理論上提出和論證了在強非局域下孤子傳輸會出現大相移現象,為邏輯門和光開關的實現提供了一個強有力的理論指導。但是Snyder模型為簡化的理想模型,在真實的物理系統中,光束的傳輸將變得更加複雜,而且理論和數值模擬表明,高階孤子不能夠穩定傳輸。在不同非局域程度下,不同非線性介質中的光孤子的傳輸性質以及孤子間的相互作用的研究已取得了很大的成果
孤子(Soliton)又稱孤立波,是一種特殊形式的超短脈衝,或者說是一種在傳播過程中形狀、幅度和速度都維持不變的脈衝狀行波。有人把孤子定義為:孤子與其他同類孤立波相遇后,能維持其幅度、形狀和速度不變。
孤子這個名詞首先是在物理的流體力學中提出來的。1834年,美國科學家約翰·斯科特·羅素觀察到這樣一個現象:在一條窄河道中,迅速拉一條船前進,在船突然停下時,在船頭形成的一個孤立的水波迅速離開船頭,以每小時14~15km的速度前進,而波的形狀不變,前進了2~3km才消失。他稱這個波為孤立波。
其後,1895年,卡維特等人對此進行了進一步研究,人們對孤子有了更清楚的認識,並先後發現了聲孤子、電孤子和光孤子等現象。從物理學的觀點來看,孤子是物質非線性效應的一種特殊產物。從數學上看,它是某些非線性偏微分方程的一類穩定的、能量有限的不彌散解。即是說,它能始終保持其波形和速度不變。孤立波在互相碰撞后,仍能保持各自的形狀和速度不變,好像粒子一樣,故人們又把孤立波稱為孤立子,簡稱孤子。
1973年,孤立波的觀點開始引入到光纖傳輸中。在頻移時,由於折射率的非線性變化與群色散效應相平衡,光脈衝會形成一種基本孤子,在反常色散區穩定傳輸。由此,逐漸產生了新的電磁理論——光孤子理論,從而把通信引向非線性光纖孤子傳輸系統這一新領域。光孤子(soliton)就是這種能在光纖中傳播的長時間保持形態、幅度和速度不變的光脈衝。利用光孤子特性可以實現超長距離、超大容量的光通信。1980年Bell試驗室Mollenewor等人首次在試驗室中觀察到了光孤子。
光孤子(Soliton,Solitons in optical fibres)是指經過長距離傳輸而保持形狀不變的光脈衝。一束光脈衝包含許多不同的頻率成分,頻率不同,在介質中的傳播速度也不同,因此,光脈衝在光纖中將發生色散,使得脈寬變寬。但當具有高強度的極窄單色光脈衝入射到光纖中時,將產生克爾效應,即介質的折射率隨光強度而變化,由此導致在光脈衝中產生自相位調製,使脈衝前沿產生的相位變化引起頻率降低,脈衝后沿產生的相位變化引起頻率升高,於是脈衝前沿比其後沿傳播得慢,從而使脈寬變窄。當脈衝具有適當的幅度時,以上兩種作用可以恰好抵消,則脈衝可以保持波形穩定不變地在光纖中傳輸,即形成了光孤子,也稱為基階光孤子。若脈衝幅度繼續增大時,變窄效應將超過變寬效應,則形成高階光孤子,它在光纖中傳輸的脈衝形狀將發生連續變化,首先壓縮變窄,然後分裂,在特定距離處脈衝周期性地復原。
光孤子的特點決定了它在通信領域的應用前景。通常將基階光孤子用於通信,因為它在整個傳播過程中沒有任何變化。光孤子通信具有以下特點:
(1)容量大:傳輸碼率一般可達20Gb/s,最高可達100Gb/s以上;
(2)誤碼率低、抗干擾能力強:基階光孤子在傳輸過程中保持不變及光孤子的絕熱特性決定了光孤子傳輸的誤碼率大大低於常規光纖通信,甚至可實現誤碼率低於10-12的無差錯光纖通信;
光孤子理論的出現,對於現代通信技術的發展起到了里程碑的作用。因為現代通信技術的發展一直朝著兩個方向努力,一是大容量傳輸,二是延長中繼距離。光孤子傳輸不變形的特點決定了它在通信領域裡應用的前景。普通的光纖通信必須每隔幾十千米設一個中繼站,經過對信號脈衝整形,放大、誤碼檢查后再發射出去,而用光孤子通信則可不用中繼站,只要對光纖損耗進行增益補償,即可把光信號無畸變地傳輸到極遠的地方。最新的實驗表明,光孤子在10Gbit/s的碼率下保持的距離超過了106km,而且傳輸的速率極高,預計可達100Gbit/s以上,因此光孤子通信無疑是實現超長距離、高速率通信的重要手段,被認為第五代光纖通信系統。
光孤子是由光纖中兩種最基本的物理現象,即群速度色散(GVD)和自相位調製(SPM)共同作用形成的。
光脈衝在光纖中傳輸時總是存在一定的頻率範圍,在線性近擬中,常將光脈衝表示成在一定範圍內一系列簡諧波的疊加。由於各諧波分量相速度不同,因而光脈衝包絡的傳輸通常以群速vg=dω/dβ來表示(β為光波波數, ω為載波頻率)。由該式可見,群速度是隨著頻率的變化而變化的,而光脈衝中不同頻率的分量則會以不同的速度進行傳播,導致脈衝的分散,這種現象稱之為群速度色散(GVD)。研究的結果表明,λd=1310nm處為零色散波長,λ>λd稱之為反常色散區域,λ<λd稱之為正常色散區域。正常與反常色散區域光脈衝的傳輸特性是不同的,在反常色散區域,光脈衝的高頻分量(藍移)較低頻分量(紅移)傳輸得快,而在正常色散區域,情況正好相反。由於傳輸情況不同,群速度色散效應不同,最終導致了光脈衝的展寬。
自相位調製效應是光波在光纖中傳輸時光波本身引起的相移。其起源於光纖的折射率n與電場強度I之間的非線性效應—克爾(kerr)效應,即:。上式中,n=1.45是線性折射率,為非線性折射率係數。由上式可知,不同強度的脈衝分量相速度是不同的,這樣,在光脈衝傳輸的過程中將會產生不同的相移,結果會造成脈衝譜的變化。例如,通過對於高斯脈衝的分析表明,自相位調製會導致脈衝前沿譜紅移,后沿譜藍移,對其它形狀脈衝的分析也有類似的結果。另外,相對在群速度色散(GVD)的反常色散區,脈衝的高頻(藍移)分量運動速度要高於低頻(紅移)分量,而自相位調製(SPM)效應所導致的脈衝前沿譜紅移又使脈衝前沿運動速度減慢和脈衝后沿由於譜藍移而加快運動速度,進而使得脈衝變窄,正好與群速度色散在反常色散區的脈衝展寬的趨勢相對應。因此,當這兩種作用在數量上達到平衡時,光脈衝就會保持不變而成為光孤粒子,即光孤子。所以說,光孤子的形成機理是光纖中群速度色散和自相位調製效應在反常色散區的精確平衡。
1895年,Korteweg和Vries提出了著名的KDV方程,從而建立了孤子的數學模型。後來經過漫長的時間,直到1973年,美國威蘇康星大學的A.C.Scott等人提出孤子的正式定義:孤子是非線性波動方程的一個孤子波解,它可傳播很長的距離而不變形,當它與其它同類孤立波相遇后,保持其幅度、形狀和速度不變。
其光孤子的概念還可進一步概括為:某一相干光脈衝在通過光纖時,脈衝前沿部分作用於光纖使之激活,而其後沿部分則受到光纖的作用獲得增益,前沿失去的和后沿獲得的能量相互抵消。其結果使得光脈衝傳輸時,沒有任何形狀上的變化,即形成一個穩定的光孤子。
光孤子通信系統的基本組成
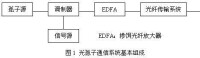
光孤子通信系統的基本組成
附圖中的孤子源並非嚴格意義上的孤子激光器,只是一種類似孤子的超短光脈衝源,它產生滿足基本光孤子能量、頻譜等要求的超短脈衝,這種超短光脈衝,在光纖中傳輸時自動壓縮、整形而形成光孤子。電信號脈衝源通過調製器將信號載干光孤子流上,承載的光孤子流經EDFA放大後進入光纖傳輸。沿途需增加若干個光放大器,以補償光脈衝的能量損失。同時需平衡非線性效應與色散效應,最終保證脈衝的幅度與形狀穩定不變。在接收端通過光孤子檢測裝置、判決器或解調器及其它輔助裝置實現信號的還原。光孤子通信走向實用的動態
研發歷程
1)1973~1980年為第一階段:首先將光孤子應用於光通信的設想是由美國貝爾實驗室的A.Hasegawa於1973年提出的,他經過嚴格的數學推導,大膽地預言了在光纖地負色散區可以觀察到光孤子的存在,並率先開闢了這一領域的研究工作,拉開了這一階段以理論研究的序幕。
2)1981~1990年為第二階段:主要工作是關鍵部件的研製。自從70年代初提出光孤子的概念以來,由於以後的十多年未能有效地觀察到光孤子的存在,直到1983年,美國貝爾實驗室的Mollenauer研究小組首次研製成功了第一支色心鎖模孤子激光器CCL,從而揭開了實驗研究的序幕。
3)1991年後為第三階段:主要工作是建立實驗系統並向實際應用邁進。在這階段,半導體激光器和EDFA在光孤子通信試驗系統中的成功應用,拉開了光孤子通信走向實用化的序幕。科學家認為,21世紀初,全光通信將走向實用化。
發展前景
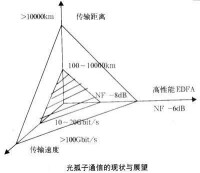
光孤子通信的現狀與展望