冗餘碼
冗餘碼
冗餘碼是一種所用符號數或信號碼元數比表示信息所必需的數目多的代碼,應用了冗餘加密技術,即利用了糾錯碼的編碼原理,在加密的文件中加入了大量的冗餘信息,從而達到加密的目的。目前,大多數研究人員研究的冗餘加密技術是公鑰密碼系統。目前,常用的冗餘編碼有漢明碼、循環碼、BCH碼、代數幾何碼等,內容非常豐富,涉及的領域廣泛。國內外很多學者利用冗餘碼的特點和理論構造了各種各樣的公鑰密碼體制、數字簽名方案、秘密共享方案、認證碼等,使相關的研究得到了迅速的發展。
冗餘碼是一種利用了糾錯碼的編碼原理,在加密的文件中加入了大量的冗餘信息,得到的一種所用符號數或信號碼元數比表示信息所必需的數目多的代碼。目前,大多數研究人員研究的冗餘加密技術是公鑰密碼系統的。
冗餘碼加密不論是在糾錯編碼研究領域還是在加密領域都是一個新的值得研究的課題,使得糾錯碼和密碼學相結合的研究緊密的結合。在對明文進行冗餘加密方面的研究,目前還有許多值的探索的東西,同時也可以促進加密方法實現多元化,不僅僅限於目前廣為應用的幾種加密方法。
循環校驗碼(CRC碼),是數據通信領域中最常用的一種差錯校驗碼,其特徵是信息欄位和校驗欄位的長度可以任意選定。
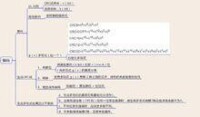
CRC生成
根據應用環境與習慣的不同,CRC又可分為以下幾種標準:
1)CRC-12碼;
2)CRC-16碼;
3)CRC-CCITT碼;
4)CRC-32碼。
CRC-12碼通常用來傳送6-bit字元串。
CRC-16及CRC-CCITT碼則是用來傳送8-bit字元串,其中CRC-16為美國採用,而CRC-CCITT為歐洲國家所採用。CRC-32碼大都被採用在一種稱為Point-to-Point的同步傳輸中。
海明碼是由1950年由漢明首先提出的,由於海明碼可以糾一位錯的線性分組碼,而且它的編碼結構和原理較為簡單,因此在數據傳輸和計算機存儲系統中廣泛應用。但是同時,海明碼的最小碼距為3,可以糾正一位錯誤,但對於兩位錯不能檢測,因此即使發生一位錯誤的幾率比較高,但在有較高要求的應用中,海明碼一般不被使用。
海明碼是一種可以糾正一位差錯的編碼。它是利用在信息位為k位,增加r位冗餘位,構成一個n=k+r位的碼字,然後用r個監督關係式產生的r個校正因子來區分無錯和在碼字中的n個不同位置的一位錯。它必需滿足以下關係式:2>=n+1 或 2 >=k+r+1
海明碼的編碼效率為:R=k/(k+r),式中k為信息位位數,r為增加冗餘位位數。
海明碼的校驗矩陣中冗餘信息較多,同時在7位的海明碼中只存在著4位的信息位,只佔其中的4/7,而且7位的海明碼只能糾正4位信息位中的一位錯誤。所以,這裡我們試驗漢明碼對連續多位差錯糾正的實現。如果不想再加大碼的距離,同時又可以糾正連續多位差錯,提高破解密文的複雜性,可根據校驗矩陣得出的漢明碼重新進行組織排列。以16比特的漢明碼為例作說明,首先把11個位元組的數據信息比特的16個位元組漢明碼后再按高低位元組分成兩組。我們將把每列的8個數據編碼每位元組8個漢明碼的第1位分別取出,組成第1個位元組。然後,再把這8個位元組漢明碼的第2位取出,組成第2個位元組。依此類推,將這組8個位元組漢明碼處理完畢,得到新的8個位元組編碼,兩組一共16位元組。我們可以看到這們排序后,每個位元組包括原來8個漢明碼的其中1位。這樣,如果我們對其中的一組編碼進行人為的糾錯,使某一編碼位元組連續8位都發生改變,實際是分別使原來8個漢明碼的其中1位發生了改變。只要在糾錯前把受干擾的編碼恢復為原來正常的排列順序,就可通過計算校驗碼完成差錯的定位及糾錯。
BCH碼是1959年由Hocquenghon,1960年由Bose和Ray-Chaud-hui分別獨立得到的糾多個隨機錯誤的循環碼。BCH碼是迄今為止發現的一類性能優良的線性糾錯碼,它的糾錯能力強,並且構造方便,編解碼簡單,有快速的解碼方法。特別是它具有嚴格的代數結構,因此它在編碼理論與實際中起著重要的作用,也是迄今為止研究的最為詳盡,分析的最為透徹,取得的成果最為豐富的碼類,並且可以用它構造某些密碼體制和認證碼。
BCH碼是循環碼種的一種,是糾正多個隨機錯誤的線性分組碼,是建立在有限域基礎之上的,有著嚴格的代數結構。不僅在理論上有重要意義,而且再實踐中,也是被廣泛應用的。
計算機採用二進位數。在計算機內部,表現為元器件的高低電位信號,分別用1和0表示。數據沿著數據通路,從源部件傳送到目的部件時,若源部件發送了某一信息(例如低電平0),而目的部件接收的信息與之不同(高電平1),則出現了錯誤。在此情況下,計算機繼續工作只會得出錯誤的結果。導致信息出錯的原因很多,主要有元器件的質量問題、電路故障和雜訊干擾等引起的錯誤。人們儘可能嚴格測試、篩選裝機的元器件,提高系統裝配工藝與質量,改善系統的抗干擾能力;但所有這一切都不可能完全避免故障,都難以使系統的平均故障間隔時間達到滿意的水平。因此,信息編碼的容錯技術是至關重要的。
信息編碼的容錯計算技術的基本思想是信息冗餘(Message Redundancy),即在信息編碼上附加一段冗餘編碼,使信息具有發現本身錯誤的能力,甚至能指出錯誤的所在位置,然後藉助邏輯線路自動糾正。利用冗餘碼實現對數據信息的校驗,目的就是提高計算機的可靠性,儘可能提高系統的平均故障間隔時間。
現有的冗餘碼加密只適用於密文中冗餘信息所佔比例較少的情況,不適合對文字較多的報價單進行加密,這一點還需要進一步改進。
正常破解時,每塊密文信息塊都要找到其中的冗餘信息,都需要進行糾錯,接受方必須知道每塊信息塊中冗餘信息的位置,而且這些位置可能是不同的,計算量加大,因此耗費的破解時間較多。因此,可以設計一個計算每塊信息中冗與位信息的程序,改進該演演算法,也是未來發展的方向。