高斯曲率
反映曲面彎曲程度的內蘊幾何量
曲面論中最重要的內蘊幾何量。設曲 面在P點處 的兩個主曲率為k1,k2,它們的乘積k=k1·k2稱為曲面 於該點的總曲率或高斯曲率。它反映了曲面的一般彎曲程度。高斯曲率k的絕對值有明顯的幾何意義。設Δб是曲面上包含P點的一小片曲面(其面積仍用Δб表示),把Δб上的每點的單位法向量n平移到E3的原點O處,那麼n的終點 的軌跡是 以O為中心的單位球面 S2上的一塊區域 Δб* 。這個對應稱為高斯映射。曲面在P點鄰近彎曲程度可用Δб*( 其面積仍用Δб*表示)與Δб的面積比刻畫。
利用隱函數定理將曲面用二元函數f的圖像來表示,並且假設點p為臨界點,也即f在該點的梯度為0(這總是可以通過適當的剛體運動來實現)。然後p點的高斯曲率就是f在點p的 黑塞矩陣(二階導數組成的2x2矩陣)的行列式。這個定義只要用基本的微積分知識就可以理解杯底或者帽頂“對應”鞍點的區別。
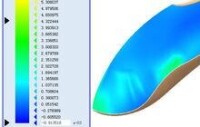
典型的高斯曲率分析結果
曲面質量和連接情況的主要依據。當曲面的高斯曲率變化比較大比較快的時候表面曲面內部變化比較大也就意味這曲面的光滑程度越低,而兩個連接的曲面如果在公共邊界上的高斯曲率發生突變就表示兩個曲面的高斯曲率並不連續,通常也叫曲率不連續,說明兩個曲面的連接沒有到達G2連接質量。
在三維CAD軟體中,通常都是使用曲面表面的顏色分佈和變化來表示曲面高斯曲率的分佈,比如ProE軟體便是如此,通過這些顏色的變化就可以直觀地知道曲面的高斯曲率的變化,而顏色的突變就表示高斯曲率的突變。