突變論
突變論
突變論是研究自然界和人類社會中連續漸變如何引起突變或飛躍,并力求以統一的數學模型來描述,預測並控制這些突變或飛躍的一門學科。它把人們關於質變的經驗總結成數學模型,表明質變既可通過飛躍的方式,也可通過漸變的方式來實現,並給出了兩種質變方式的判別方法,它還表明,在一定情況下,只要改變控制條件,一個飛躍過程可以轉化為漸變,而一個漸變過程又可轉化為飛躍。突變論認為事物結構的穩定性是突變論的基礎,事物的不同質態從根本上說就是一些具有穩定性的狀態,這就是為什麼有的事物不變,有的漸變,有的則突變的內在原因。在嚴格控制條件的情況下,如果質變經歷的中間過渡狀態是不穩定的,它就是一個飛躍過程; 如果中間狀態是穩定的,它就是一個漸變過程。
“突變”一詞,法文原意是“災變”,是強調變化過程的間斷或突然轉換的意思。突變論的主要特點是用形象而精確的數學模型來描述和預測事物的連續性中斷的質變過程。
突變論是一門著重應用的科學,它既可以用在“硬”科學方面,又可以用於“軟”科學方面。在數學上突變論屬於微分流形拓撲學的一個分支,是關於奇點的理論。它可以根據勢函數而把臨界點分類,並且研究各種臨界點附近的非連續現象的特徵。

突變論
因為英文 catastrophe一詞的原意為突然來臨的災禍,所以也有把它譯作災變論。突變論一般並不給出產生突變機制的假設,而是提供一個合理的數學模型來描述現實世界中產生的突變現象,對它進行分類,使之系統化。突變論特別適用於研究內部作用尚屬未知、但已觀察到有不連續現象的系統。
突變論最初由荷蘭植物學家和遺傳學家德弗里斯(Hugo Marie de Vrier,1848~1935)提出。他根據進行多年的月見草(Oenthera lamarckiana)實驗的結果,於1901年提出生物進化起因於驟變的‘突變論’,歷史上曾發生了重大影響,使許多人對達爾文的漸變進化論產生了懷疑。但後來的研究表明,月見草的驟變是較為罕見的染色體畸變所致,並非進化的普遍規律。
後來突變論被重新定義和提出,它是20世紀60年代末法國數學家R.托姆為了解釋胚胎學中的成胚過程而提出來的。1967年托姆發表《形態發生動力學》一文,闡述突變論的基本思想,1969年發表《生物學中的拓撲模型》,為突變論奠定了基礎。1972年發表專著《結構穩定與形態發生》,系統地闡述了突變論。70年代以來,E.C.塞曼等人提出著名的突變機構,進一步發展了突變論,並把它應用到物理學、生物學、生態學、醫學、經濟學和社會學等各個方面,產生了很大影響。
從I.牛頓和G.W.萊布尼茲時代以來得到很大發展的微積分學,一般只考慮光滑的連續變化的過程,而突變論則研究跳躍式轉變、不連續過程和突發的質變。突變論的基礎是結構穩定性。結構穩定性反映同種物體在形態上千差萬別中的相似性。例如,人的面貌雖因歲月流逝而發生變化,但仍存在區別於他人的特徵。結構穩定的喪失,就是突變的開始。突變論的基本概念是靜態模型,它把形態按結構穩定特徵分類。至於描述結構變化的動力學理論,至今仍不完備。
突變論
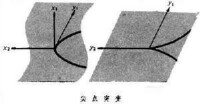
1955年H·惠特尼在研究這種映射的特點時,得出兩類一般奇點。一類是摺疊,可用公式y1=x剮,y2=x2表示。把球面投射到平面上,赤道上的點產生的奇點就是這種奇點。另一類是尖點,局部坐標可寫成y1=x劅+x1x2,y2=x2。把空間曲面y1=x劅+x1x2投影到平面(y1,y2)上,平面上有一半立方拋物線,在原點處有一個尖點 (見圖)。曲線把平面分成兩部分,較小部分的原像均由三點構成,而較大部分只由一個點構成。在尖點處映射引起突變,這是突變論所研究的最常見的一種突變。
惠特尼證明,尖點是穩定的,也就是在這種映射附近的映射在適當的地方也有同類的奇點。
突變論的創始人是法國數學家雷內托姆,他於1972年發表的《結構穩定性和形態發生學》一書闡述了突變理論,榮獲國際數學界的最高獎---菲爾茲獎章。突變論的出現引起各方面的重視,被稱之為“是牛頓和萊布尼茨發明微積分三百年以來數學上最大的革命”。
在自然界和人類社會活動中,除了漸變的和連續光滑的變化現象外,還存在著大量的突然變化和躍遷現象,如水的沸騰、岩石的破裂、橋樑的崩塌、地震、細胞的分裂、生物的變異、人的休克、情緒的波動、戰爭、市場變化、經濟危機等等。突變論方法正是試圖用數學方程描述這種過程。突變論的研究內容簡單地說,是研究從一種穩定組態躍遷到另一種穩定組態的現象和規律。
突變論認為,系統所處的狀態,可用一組參數描述。當系統處於穩定態時,標誌該系統狀態的某個函數就取唯一的值。當參數在某個範圍內變化,該函數值有不止一個極值時,系統必然處於不穩定狀態。雷內托姆指出:系統從一種穩定狀態進入不穩定狀態,隨參數的再變化,又使不穩定狀態進入另一種穩定狀態,那麼,系統狀態就在這一剎那間發生了突變。突變論給出了系統狀態的參數變化區域。
突變論提出,高度優化的設計很可能有許多不理想的性質,因為結構上最優,常常聯繫著對缺陷的高度敏感性,就會產生特別難於對付的破壞性,以致發生真正的“災變”。在工程建造中,高度優化的設計常常具有不穩定性,當出現不可避免的製造缺陷時,由於結構高度敏感,其承載能力將會突然變小,而出現突然的全面的塌陷。突變論不僅能夠應用於許多不同的領域,而且也能夠以許多不同的方式來應用。
通過突變論能夠有效地理解物質狀態變化的相變過程,理解物理學中的激光效應,並建立數學模型。通過初等突變類型的形態可以找到光的焦散面的全部可能形式。應用突變論還可以恰當地描述捕食者----被捕食者系統這一自然界中群體消長的現象。過去用微積分方程式長期不能滿意解釋的,通過突變論能使預測和實驗結果很好地吻合。突變論還對自然界生物形態的形成作出解釋,用新穎的方式解釋生物的發育問題,為發展生態形成學作出了積極貢獻。
突變論對哲學上量變和質變規律的深化,具有重要意義。很長時間以來,關於質變是通過飛躍還是通過漸變,在哲學上引起重大爭論,歷史上形成三大派觀點:“飛躍論”、“漸進論”和“兩種飛躍論”。突變論認為,在嚴格控制條件的情況下,如果質變中經歷的中間過渡態是穩定的,那麼它就是一個漸變過程。質態的轉化,既可通過飛躍來實現,也可通過漸變來實現,關鍵在於控制條件。
應用突變論還可以設計許許多多的解釋模型。例如經濟危機模型,它表現經濟危機在爆發時是一種突變,並且具有折迭型突變的特徵,而在經濟危機后的復甦則是緩慢的,它是經濟行為沿著“折迭曲面”緩慢滑升的漸變。此外,還有“社會輿論模型”、“戰爭爆發模型”、“人的習慣模型”、“對策模型”、“攻擊與妥協模型”等等。
突變論能解說和預測自然界和社會上的突然現象,無疑它也是軟科學研究的重要方法和得力工具之一。突變論在數學、物理學、化學、生物學、工程技術、社會科學等方面有著廣闊的應用前景。《大英百科年鑒》1977年版中寫道:“突變論使人類有了戰勝愚昧無知的珍奇武器,獲得了一種觀察宇宙萬物的深奧見解”。
自然,突變論的應用在某些方面還有待進一步的驗證,在將社會現象全部歸結為數學模型來模擬時還有許多技術細節要解決,在參量的選擇和設計模型方面還有大量工作要做。此外,突變理論本身也還有待於進一步完善,在突變論的方法上也有許多爭議之處。
總之,突變論問世以來,引起褒貶不一的評述,正象任何一門新興學科的發展經歷一樣。著名數學家斯圖爾特客觀地評價了突變論,他寫道:“適當地理解突變理論,可以為我們生存的世界提供新穎而深入的見解。但它還需要加以發展、檢驗、修改,經歷一般成為可靠的科學工具的全部過程。但我毫不懷疑,也不是宇宙中的唯一事物”。
突變論在許多領域已經取得了重要的應用成果。隨首研究的深入,它的應用範圍在不斷擴大,相信它在我國四化建設中將發揮重要作用。
資訊理論將信息的傳遞作為一種統計現象來考慮,給出了估算通信通道容量的方法。信息傳輸和信息壓縮是資訊理論研究中的兩大領域。這兩個方面又由信息傳輸定理、信源-通道隔離定理相互聯繫。
什麼是 信息?
信息現代定義。[2006年,醫學信息(雜誌),鄧宇等].
信息是 物質、能量、信息及其屬性的標示。逆維納信息定義
信息是 確定性的增加。逆香農信息定義
信息是 事物現象及其屬性標識的集合。2002年
控制論
是研究動物(包括人類)和機器內部的控制與通信的一般規律的學科,著重於研究過程中的數學關係
主要研究遠離平衡態的開放系統在與外界有物質或能量交換的情況下,如何通過自己內部協同作用,自發地出現時間、空間和功能上的有序結構。協同論以現代科學的最新成果——系統論、資訊理論、控制論、突變論等為基礎,吸取了結構耗散理論的大量營養,採用統計學和動力學相結合的方法,通過對不同的領域的分析,提出了多維相空間理論,建立了一整套的數學模型和處理方案,在微觀到宏觀的過渡上,描述了各種系統和現象中從無序到有序轉變的共同規律。
協同論是研究不同事物共同特徵及其協同機理的新興學科,是近十幾年來獲得發展並被廣泛應用的綜合性學科。它著重探討各種系統從無序變為有序時的相似性。協同論的創始人哈肯說過,他把這個學科稱為“協同學”,一方面是由於我們所研究的對象是許多子系統的聯合作用,以產生宏觀尺度上結構和功能;另一方面,它又是由許多不同的學科進行合作,來發現自組織系統的一般原理。
是研究系統的一般模式,結構和規律的學問,它研究各種系統的共同特徵,用數學方法定量地描述其功能,尋求並確立適用於一切系統的原理、原則和數學模型,是具有邏輯和數學性質的一門新興的科學。