突變理論

“突變”一詞，法文原意是“災變”，強調變化過程的間斷或突然轉換的意思。在自然界和人類社會活動中，除了漸變的和連續光滑的變化現象外，還存在著大量的突然變化和躍遷現象，如岩石的破裂、橋樑的崩塌、地震、海嘯、細胞的分裂、生物的變異、人的休克、情緒的波動、戰爭、市場變化、企業倒閉、經濟危機等。

突變理論研究的是從一種穩定組態躍遷到另一種穩定組態的現象和規律。它指出自然界或人類社會中任何一種運動狀態，都有穩定態和非穩定態之分。在微小的偶然擾動因素作用下，仍然能夠保持原來狀態的是穩定態；而一旦受到微擾就迅速離開原來狀態的則是非穩定態，穩定態與非穩定態相互交錯。非線性系統從某一個穩定態（平衡態）到另一個穩定態的轉化，是以突變形式發生的。突變理論作為研究系統序演化的有力數學工具，能較好地解說和預測自然界和社會上的突然現象，在數學、物理學、化學、生物學、工程技術、社會科學等方面有著廣闊的應用前景。

突變理論是用形象的數學模型來描述連續性行動突然中斷導致質變的過程，這一理論與混沌理論（Chaos Theory）相關，儘管它們是兩個完全獨立的理論，但現在突變理論被普遍視作為混沌理論的一部分。

儘管突變理論是一門數學理論，它的核心思想卻有助於人們理解系統變化和系統中斷。如果系統處於休止狀態（也就是說，沒有發生變化），它就會趨於獲得一種理想的穩定狀態，或者說至少處在某種定義的狀態範圍內。如果系統受到外界變化力量作用，系統起初將試圖通過反作用來吸收外界壓力。如果可能的話，系統隨之將恢復原先的理想狀態。如果變化力量過於強大，而不可能被完全吸收的話，突變（Catastrophic Change）就會發生，系統隨之進入另一種新的穩定狀態，或另一種狀態範圍。在這一過程中，系統不可能通過連續性的方式回到原來的穩定狀態。

試舉一例，更為形象地解釋這一理論。讓人們假想有一隻玻璃瓶放在桌面上，它處在一個穩定的狀態，沒有任何變化，此為穩定平衡（Stable Equilibrium）。現在假想用你的手指輕推瓶頸，不要太用力。這時變化產生，玻璃瓶晃動起來，它在通過一種連續性的方式來吸收變化，此為不穩定平衡（Unstable Equilibrium）。如果你停止推力，玻璃瓶將恢復到它的理想穩定狀態。然而，如果你繼續用力推下去，在你的推力達到一定程度的時候，玻璃瓶便會倒下，由此又進入了一種新的穩定平衡狀態。玻璃瓶的狀態在這一瞬間就發生了突變，一個非連續性的變化就這樣產生了：在玻璃瓶下跌的過程中，沒有任何可能的穩定中間狀態，直到它完全倒伏在桌面上為止。

Thorn的突變理論意味著，系統變化是通過連續性的和非連續性的兩種變化模式來實現的。這一過程與混沌理論相關之處在於，玻璃瓶只存在兩種狀態——要麼站立，要麼躺倒。這兩種狀態也就是可能的結果池（Outcome Basins），參見：混沌理論。然而，還有一些狀態永遠不可能被達到，因為它們具有內在的不穩定性。

7種初等突變：折迭型突變（Fold Catastrophe）、尖點型突變（Cusp Catastrophe）、燕尾型突變（Swallowtail Catastrophe）、蝴蝶型突變（Butterfly Catastrophe）、雙曲型臍點（Hyperbolic Umbilic）、橢圓型臍點（Elliptic Umbilic）和拋物型臍點（Parabolic Umbilic）。

突變理論的次級應用研究包括：歧變理論（Bifurcation Theory）、非平衡熱力學（Nonequilibrium Thermodynamics）、奇點理論（Singularity Theory）、協同論（Synergetics）及拓撲動力學（Topological Dynamics）等。

現在被視為混沌理論（Chaos Theory）一部分的突變理論，起源於20世紀60年代末。1972年，法國數學家René Thom發表著作對這一理論進行了獨立且系統的闡述。他的這部著作名為：《結構穩定性和形態發生學》（Structural Stability and Morphogenesis），Thom希望能夠籍此預測複雜無序的系統變化行為。20世紀70年代，英國數學家E. C. Zeeman對突變理論的發展應用做了進一步的研究。

許多年來，自然界許多事物的連續的、漸變的、平滑的運動變化過程，都可以用微積分的方法給以圓滿解決。例如，地球繞著太陽旋轉，有規律地周而復始地連續不斷進行，使人能極其精確地預測未來的運動狀態，這就需要運用經典的微積分來描述。但是，自然界和社會現象中，還有許多突變和飛躍的過程，飛越造成的不連續性把系統的行為空間變成不可微的，微積分就無法解決。例如，水突然沸騰，冰突然融化，火山爆發，某地突然地震，房屋突然倒塌，病人突然死亡……。

這種由漸變、量變發展為突變、質變的過程，就是突變現象，微積分是不能描述的。以前科學家在研究這類突變現象時遇到了各式各樣的困難，其中主要困難就是缺乏恰當的數學工具來提供描述它們的數學模型。那麼，有沒有可能建立一種關於突變現象的一般性數學理論來描述各種飛躍和不連續過程呢？這迫使數學家進一步研究描述突變理論的飛躍過程，研究不連續性現象的數學理論。1972年法國數學家勒內·托姆在《結構穩定性和形態發生學》一書中，明確地闡明了突變理論，宣告了突變理論的誕生。

突變理論主要以拓撲學為工具，以結構穩定性理論為基礎，提出了一條新的判別突變、飛躍的原則：在嚴格控制條件下，如果質變中經歷的中間過渡態是穩定的，那麼它就是一個漸變過程。

比如拆一堵牆，如果從上面開始一塊塊地把磚頭拆下來，整個過程就是結構穩定的漸變過程。如果從底腳開始拆牆，拆到一定程度，就會破壞牆的結構穩定性，牆就會嘩啦一聲，倒塌下來。這種結構不穩定性就是突變、飛躍過程。

又如社會變革，從封建社會過渡到資本主義社會，法國大革命採用暴力來實現，而日本的明治維新就是採用一系列改革，以漸變方式來實現。

對於這種結構的穩定與不穩定現象，突變理論用勢函數的窪存在表示穩定，用窪取消表示不穩定，並有自己的一套運算方法。例如，一個小球在窪底部時是穩定的，如果把它放在突起頂端時是不穩定的，小球就會從頂端處，不穩定滾下去，往新窪地過渡，事物就發生突變；當小球在新窪地底處，又開始新的穩定，所以勢函數的窪存在與消失是判斷事物的穩定性與不穩定性、漸變與突變過程的根據。

托姆的突變理論，就是用數學工具描述系統狀態的飛躍，給出系統處於穩定態的參數區域，參數變化時，系統狀態也隨著變化，當參數通過某些特定位置時，狀態就會發生突變。

突變理論提出一系列數學模型，用以解釋自然界和社會現象中所發生的不連續的變化過程，描述各種現象為何從形態的一種形式突然地飛躍到根本不同的另一種形式。如岩石的破裂，橋樑的斷裂，細胞的分裂，胚胎的變異，市場的破壞以及社會結構的激變……。

按照突變理論，自然界和社會現象中的大量的不連續事件，可以由某些特定的幾何形狀來表示。托姆指出，發生在三維空間和一維空間的4個因子控制下的突變，有7種突變類型：折迭突變、尖頂突變、燕尾突變、蝴蝶突變、雙曲臍突變、橢圓臍形突變以及拋物臍形突變。

例如，用大拇指和中指夾持一段有彈性的鋼絲，使其向上彎曲，然後再用力壓鋼絲使其變形，當達到一定程度時，鋼絲會突然向下彎曲，並失去彈性。這就是生活中常見的一種突變現象，它有兩個穩定狀態：上彎和下彎，狀態由兩個參數決定，一個是手指夾持的力(水平方向)，一個是鋼絲的壓力(垂直方向)，可用尖頂突變來描述。

尖頂突變和蝴蝶突變是幾種質態之間能夠進行可逆轉的模型。自然界還有些過程是不可逆的，比如死亡是一種突變，活人可以變成死人，反過來卻不行。這一類過程可以用折迭突變、燕尾突變等時函數最高奇次的模型來描述。所以，突變理論是用形象而精確的得數學模型來描述質量互變過程。

英國數學家奇曼教授稱突變理論是“數學界的一項智力革命——微積分后最重要的發現”。他還組成一個研究團體，悉心研究，擴展應用。短短几年，論文已有400多篇，可成為盛極一時。

托姆曾於1958年榮獲國際數學界的最高獎——菲爾茲獎。

突變理論廣泛應用於變革管理和組織發展領域。有一種變化形式是平滑的、持續的和遞增的。業務流程改進的一系列創意多遵循這一變化模式，例如改善(Kaizen)、全面質量管理(Total Quality Management)及六西格瑪（Six Sigma）。用突變理論術語來說，就是一種基於現有穩定界面的的預設變化。

還有一種變化形式則是災難性的、突發的、激進的，徹底背離變化前的狀態。這種變化結果往往是業務流程重組(Business Process Reengineering)這類劇烈的變革行為造成的。這種類型的變化是“非連續的”，用突變理論術語來說，它是全新定義另一個穩定狀態的突變。

因此，“真正的”的變化更類似於企業流程重組這樣的劇烈變革，此外，當然也還有簡單的變革，採用什麼樣的變革取決於具體問題的需要。變革專家所面對的挑戰正在於此，他們必須能夠決定何時需要激進變革，而何時又該執行漸進變革。做出正確選擇並不容易，因為激進變革必然導致組織經歷一段時期的“混亂無序”，在此之後，新的穩定狀態才能被發現和定義下來。這就得用到變革管理中的融凍法（Unfreezing/Freezing Method）。有些情況下，組織會被強加以激進變革。而且，現實中可能根本就不存在那麼一條“從哪裡來，到哪裡去”的清晰路徑，引領組織持續漸進變革。在這種情況下，假設的變革路線也就毫無意義。

1．突變理論有助於認識變革管理的真實面貌、理解混沌理論的思想觀點。它揭示了為什麼真正的變革是一項危險活動。

2．突變理論打斷了“組織能夠基於多樣化的價值頻譜表現出各種形態”的念頭，大概只存在幾個有限的真正意義上的穩定組織形態。

3．突變理論同樣揭示了為什麼變革不可以被“管理”，而只能被“影響”。

4．理論應付“形式”形式的思想(Gestalt格式塔理論)和變動。它開創了認識組織的新視角。

1、從認識組織行為的角度來看，托姆的研究工作的意義目前更多地體現在定性分析上，而非定量分析。

2．即便是預測最簡單的系統行為，仍然具有挑戰性。

3．考慮到研究的時間限，所以一切都不是“突變”，只是多種因素的積累效應在某一刻凸顯時被研究者所捕捉。

4．托姆的研究工作未能涉及具有多個（5個以上）重要變數的複雜系統，也許根本就不可能對複雜系統（或組織）行為進行預測。

企業自身成長中的不確定性和經營環境的不確定性，突如其來的失敗或萎縮成為時代的特徵，這使得人們越來越傾向於從系統論的角度，將企業視為非線性系統和複雜系統，並應用非線性系統理論，分析企業發展的規律，探討企業演化的模式和與環境的互動關係。

20世紀60年代，隨著系統論的興起，系統管理理論引起管理學者和企業家的廣泛關注。孔茨（Koontz）認為，“不論是管理著作，還是從事實務的主管人員，都不應該忽視系統方法”，斯科特（Scott）則將系統理論的引入看作是管理理論有別於傳統企業發展理論的真正革命。

系統論主要有三大思想體系：耗散結構理論、協同論和突變理論。其中，突變理論可以為組織提供一系列關於組織發展過程中不確定性對其影響的系統分析。談到突變論時，有必要指出早於托姆的德弗里斯以及他的突變進化論。

多年以來，如何看待世界，存在兩種截然對立的觀點，達爾文主要從“漸變”或“連續性”的角度考察世界，認為自然界的演變是十分緩慢的，這種“漸變論”是當時學術界的主導思想。然而，19世紀末，以達爾文進化論為基礎的連續變異進化觀，既無法解釋古生物學中大量存在的“化石斷層”現象，亦無從說明變異的遺傳本質，正是在這一背景下，荷蘭植物學家雨果·德弗里斯 (Hugo De Vries，1848-1935)建立了以“物種的突發產生”為主要內容的進化學說突變論。

他在1889年出版了《細胞內泛生論》，以批判的眼光回顧了以前在遺傳方面的研究，提出了細胞核的成分“泛生子”（Pangenes）決定遺傳特性。1901-1903年，他撰寫出版了《突變論》一書，集中闡述了他的生物突變論思想。德弗里斯證明，達爾文強調的那種微小變異不是形成新物種的真正基礎，物種起源主要是通過跳躍式的變異—“突變”來完成的。他解答了達爾文學說中許多使人迷惘的問題，回擊了一些人對進化論的攻擊，從而使達爾文進化論向前推進了一大步。

德弗里斯還給出了生物突變的主要特性。它們包括：

(1) 突變的突發性。新的基本種可不經過任何中間階段而突然出現；在進化過程中，突變體的產生無法預見，新突變體一旦出現，就“具有新型式的所有性狀”；

(2) 突變的多向性。新的基本種突變的形成，是在所有的方向上發生的，所有的器官幾乎在所有可能的方向上都會發生變化；

(3) 突變的穩定性和不可逆性。從新的基本種產生的時刻起，通常是完全穩定的。突變一旦產生，就能穩定地遺傳給後代，它不具有“逐漸返回其起源形式的傾向”，這種不可逆性可導致突變體直接形成一個新物種；

(4) 突變的周期性。突變是周期性出現的，不管研究的材料及其性質是什麼，突變出現的幾率是有規律可尋。如月見草(正常型)的 7個變種出現的幾率為1%-3%；

(5) 突變的隨機性。突變可發生在生物體的任一部位，突變的發生與外界條件影響之間，新的性狀同個體的變異性之間，沒有什麼特殊的聯繫。

德弗里斯和托姆的突變論觀點具有普遍的意義，它轉換了人們認識的角度，使人們可以用非連續進化觀，進入一個迥異於連續性進化觀的世界，從而成為當今世界上應用極為廣泛的現代方法論之一。同時，突變論作為一門著重應用的科學，既可以用在“硬”科學方面，又可以用於“軟”科學方面。特別地，對洞察企業發展的演化過程，把握企業發展的規律，指導企業的經營實踐，具有重要的方法論意義和啟示作用。

企業在制定決策的時候，往往會碰到這樣的兩難抉擇：到底應該對原來的技術進行改進，還是要研發新的技術來替代？或者更一般地，企業在推行變革、再造和創新的時候，是漸進式的還是突變式的？是改良還是改革？大體而言，企業往往偏好在其熟悉的、更接近現有技術的基礎上進行技術創新，在成熟的技術上不斷改進。

涉及企業改革時亦大致如此，很多情況下大家會力主和風細雨式的漸進變革。這種想法佔上風的理由似乎很充足：企業發展要求穩，穩健發展，切忌急功近利、急躁冒進，避免出現大幅變化的“巨漲落”；要穩中求變，一步一步變化，從量變到質變，穩紮穩打，凡事要控制在平衡態，不可操之過急，否則會欲速則不達，甚至嘩變。

再則，還有路徑依賴一說，即事物演化對其發展道路和適用規則的選擇有依賴性，一旦選擇了某種道路就很難改弦易轍。然而，對改良式技術創新和漸進式變革的負面問題要有充分的認知。

改良型技術創新雖然能很快會被市場上的主流消費者所接受，但隨著技術創新的不斷改進，改良型創新可能會導致產品的性能過剩。就變革而言，漸進式的改進其實有一個根本的前提，那就是企業的發展方向是正確的，對大格局的研判是準確的。否則，南轅北轍，拾遺補缺式的改良只會導致在錯誤的道路上漸行漸遠，改良的後果只是在原本已經盤根錯節積弊深沉的系統中加劇複雜，使問題的解決變得更加困難。

漸進式變革是一種從外部來解決問題的方法，最大的問題是忽視了企業中衝突的內在動力和本質，就象在數字化技術中全力研究模擬技術的日該企業一樣，付出很多但卻無法得到回報，甚至因此而落敗。更何況，正如一位智者所言，“財富永遠來源於更好地突破現狀、把握未知，而非更好地完善已知”。人們更加倡導通過反梯度推移，實現組織的突變型再造和創新。所謂 反梯度推移，是指不是象通常那樣序貫的、順次的、梯度的推進，而是漸進過程的中斷，非平衡發展的突變和創造性毀滅（creative destruction）。

熊彼特在總結他所觀察的現代經濟演化特徵時指出，推動進步的力量，並非來自過去經驗的累積，而在於顛覆性的全盤創新。美國科學哲學家托馬斯·庫恩亦提出“範式轉移(paradigm shift)”概念，他特彆強調新舊範式之間具有不可通約性，範式的轉換是一種整體性、結構性轉換；範式的改變是世界觀的改變，範式一改變，這世界本身也隨之改變了。在轉型變革期，企業的再造和創新絕不是一次改良運動，而是重大的突變式改革。

這主要表現為以下三個方面：

（1）企業變革和再造是對固有基本信念的挑戰。這些信念是“隱藏在暗處的頑石”，深深植根於企業內部，影響企業員工的心智模式，對企業經營活動的展開、業務流程的設計和執行起基礎性作用。由於當今世界的商業環境及遊戲規則已經發生革命性的變化，從根本上動搖了以往的商業邏輯，必須對企業既有的、視為當然的基本信念進行相應的批判性審視，促進基本信念的重大轉變，使組織里的每個人都開始關心“做正確的事”而非“把事做正確”。突變型再造和創新的根本目的，是要不斷地矯正軌道，使企業永遠向著正確的方向，而非如何在現有的軌道上跑得更快。

（2）企業再造和變革不是要在業績上取得點滴的改善或逐漸提高，而是要在經營業績上取得顯著的改進。企業變革和再造要基於某一嶄新的理念而展開，不是對組織和流程簡單的修修補補，而是對組織的再造，對業務流程的重建，對“零和競爭”的超越，對新市場的開闢，從而使企業產生脫胎換骨的變化。如企業通過挖掘顧客的潛在需求，採用突變型技術取代原有的傳統技術，通過與市場意見領導者進行溝通和對消費者進行再教育等方式影響市場，採取主動性營銷策略，挖掘商機，創造新的市場格局和豐厚的新的利潤源。

（3）突變是擺脫積重難返的舊體制和複雜系統巨大慣性的唯一出路，唯有通過突變和創新，方可實現企業從舊質轉化為新質的爆髮式躍遷。在明晰事物的真相和問題的癥結后，就要大刀闊斧從容不迫地施行變革，置死地而後生，從根本上使企業走出困境。

著名的洛侖茲蝴蝶效應現象，是指事物發展的結果對初始條件和邊界條件具有極為敏感的依賴性。初始條件極小的偏差將會引起結果的巨大差異。

1979年12月29日，當美國科學家洛侖茲在華盛頓美國科學促進會，以“可預言性：一隻蝴蝶在巴西扇動翅膀會在得克薩斯引起龍捲風嗎？”為題演講的時候，人們對蝴蝶效應也許還缺少切實的體會，但隨著事物間的聯繫越來越密切，系統越來越龐大複雜，蝴蝶效應越來越顯著，發生的頻率也越來越高。

2003年北美歷史上發生了最嚴重的大停電事故，造成了60億美元的直接損失。經聯合調查小組的專家證實，其原因卻非常簡單，不過是一些長得過分茂密的樹叢使俄亥俄州克里夫蘭附近的電線短路。

在經濟全球化、一體化和信息化時代，蝴蝶效應具有更大的普遍性，不僅在自然界而且在政治、經濟、軍事、社會等人工系統，均有蝴蝶效應發生，產生的影響力和衝擊力也十分巨大。

突變理論、蝴蝶效應也給企業發展帶來了重大的影響。蝴蝶效應還改變了人們對企業的傳統認識，即企業可以在一個穩定環境中按照一個相對穩定的模式有序發展。現代企業是一個由人的因素、技術的因素和環境因素構成的多項、共時和互動的複雜系統，由於對初始條件的高度敏感性，一點細微的變化，都會引起企業的巨大變革，企業發展面臨更大的突變性和不可控制性。

在這樣一個複雜且充滿突變的時代，企業正被一些越來越細小和看起來不重要的事件所左右。一條不引人注目的小道消息，通過網際網路可能會迅速傳遍世界，蝴蝶效應使越來越多的企業被莫名其妙地捲入危機的旋渦，有些甚至因此而走向崩潰；相反，也可能因為一件事情做得恰到好處正當其時、一個主意很獨特而被大事渲染，一夜走紅，聞名天下，進而被模式化、標準化、連鎖化而坐收漁利。

在市場經濟競爭日益激烈的今天，社會分工越來越細，流程化、標準化、制式化和專業化程度越來越高，企業與企業之間在戰略、產品和服務等方面的同質化現象越來越嚴重。從這種意義上講，企業就是細節，市場的競爭就是細節上的競爭。

21世紀的商業時代，是一個以1%決定勝負的時代。在這個時代，一個細節就可以左右企業的成敗和興衰。如果說一個企業在產品或服務上注重細節的改進，也許只給用戶增加了1%的方便，然而企業得到的卻是客戶100% 的購買行為。因為當客戶做出購買決策前，自然會貨比三家，在同質市場上，相同的材料、相同的產品功能等“相同項”都被抵消了，對決策起作用的就是那1%的細節。正是1%細節的比較優勢打動了客戶，贏得了市場。這也應了密斯·凡·德羅的一句話：“魔鬼在細節”。

密斯·凡·德羅作為20世紀世界四位最偉大的建築師之一，在多個場合反覆強調指出，不管你的建築設計方案如何恢弘大氣，如果對細節的把握不到位，就不能稱之為一件好作品。細節的準確、生動可以成就一件偉大的作品；細節的疏忽會毀壞一個宏偉的規劃。

決策本質上就是把不確定性的東西加以確定。決策者要在充分論證的基礎上審時度勢，敢於拍板、敢於擔當；當斷不斷，必為所亂。在做決策的時候，不追求絕對最優的決策，轉而追求簡潔高效的滿意解甚至非劣解（Pareto解）即可。

形而上地講，最優解只存在於數學邏輯和理念中，現實世界中的最優解其實是不存在的。這不僅是因為人的理性和精力是有限的，人的“有限理性”從根本上否則了得到絕對意義上最優解的可能；而且為得到最優解通常需要足夠的信息，而信息的獲得是需要代價的。

這自然就引出一個在這些信息支持下獲得最優解產生的收益（得）與為得到這些信息本身所付出成本（失）之間的權衡問題，會不會出現“得”不償“失”的情況？再則，也是在此處要特彆強調的是，突變論指出高度優化的設計（最優解）很可能有許多不理想的性質，因為在結構上、性能上追求最優，常常魯棒性很差，穩定性不高，對方案中可能的缺陷具有高度敏感性。

最優解要求系統各部分銜接每次都準確無誤，而當系統一旦有問題（現在的系統幾乎都是多因素、共時、互動的複雜巨系統，出問題的概率是很高的！），其承載能力將會突然變小，出現突然的全面的“災變”，產生特別難於解決的破壞性，以致讓系統徹底癱瘓。

21世紀以來人類進入了網路時代，今天的經濟已是一個全球化的經濟、開放的經濟和一體化的經濟，是一個既高度分工又高度綜合集成的經濟，諸如資金、人員、管理和品牌等資源不再象以前那樣受到空間的限制，而是更加方便和自由地流動。

交通和通訊的極大便利以及IT技術和網際網路的強力滲透，把人類緊緊相連。每個企業不過是龐大網路體系中的一個節點，彼此制約，相互依賴。世界上任何一個角落的突變都會在全世界範圍內飛速傳播，衝突變理論創始人擊波迅速放大，其頻度和深度前所未有，企業將面臨更為動蕩的商業環境。

隨著信息技術的飛速發展和網路的普及，全球化、信息化和網路化正在深刻地改變世界的商業模式，使企業不得不在一個蘊含更多不確定性和突變性的商業風險和危機中打拚。在過去的幾年裡，施樂、山登、廣本、美林證券、亨氏、肯德基、寶潔、卡夫、強生、聯合利華、雀巢、哈根達斯等跨國公司，以及本土的中航油、長虹、光明乳業等都曾被捲入危機的漩渦之中。而一些曾經無限風光如日中天的企業，如美國的安然、世通、安達信，英國的巴林銀行，香港的百富勤，中國大陸的巨人、德隆、中天勤、銀廣夏、亞細亞、飛龍、巨能鈣等幾乎是在傾刻間不復存在，就像滙豐集團主席龐·約翰所說的那樣：“過去摧毀一座金融帝國可能需要一個很漫長的過程，但是現在，即使是經營了上百年的金融帝國也可以在一夜之間傾塌”。

突變理論在在自然科學的應用是相當廣泛的。在物理學研究了相變、分叉、混沌與突變的關係，提出了動態系統、非線性力學系統的突變模型，解釋了物理過程的可重複性是結構穩定性的表現。在化學中，用蝴蝶突變描述氫氧化物的水溶液，用尖頂突變描述水的液、氣、固的變化等。在生態學中研究了物群的消長與生滅過程，提出了根治蝗蟲的模型與方法。在工程技術中，研究了彈性結構的穩定性，通過橋樑過載導致毀壞的實際過程，提出最優結構設計。

突變理論在社會現象的一個用歸納為某種量的突變問題，人們施加控制因素影響社會狀態是有一定條件的，只有在控制因素達到臨界點之前，狀態才是可以控制的。一旦發生根本性的質變，它就表現為控制因素所無法控制的突變過程。還可以用突變理論對社會進行高層次的有效控制，為此就需要研究事物狀態與控制因素之間的相互關係，以及穩定區域、非穩定區域、臨界曲線的分佈特點，還要研究突變的方向與幅度。

通過突變理論能夠有效地理解物質狀態變化的相變過程，理解物理學中的激光效應，並建立數學模型。通過初等突變類型的形態可以找到光的焦散面的全部可能形式。應用突變論還可以恰當地描述捕食者----被捕食者系統這一自然界中群體消長的現象。過去用微積分方程式長期不能滿意解釋的，通過突變論能使預測和實驗結果很好地吻合。

突變論還對自然界生物形態的形成作出解釋，用新穎的方式解釋生物的發育問題，為發展生態形成學作出了積極貢獻。

突變論對哲學上量變和質變規律的深化，具有重要意義。很長時間以來，關於質變是通過飛躍還是通過漸變，在哲學上引起重大爭論，歷史上形成三大派觀點：“飛躍論”、“漸進論”和“兩種飛躍論”。突變論認為，在嚴格控制條件的情況下，如果質變中經歷的中間過渡態是穩定的，那麼它就是一個漸變過程。質態的轉化，既可通過飛躍來實現，也可通過漸變來實現，關鍵在於控制條件。

應用突變論還可以設計許許多多的解釋模型。例如經濟危機模型，它表現經濟危機在爆發時是一種突變，並且具有折迭型突變的特徵，而在經濟危機后的復甦則是緩慢的，它是經濟行為沿著“折迭曲面”緩慢滑升的漸變。此外，還有“社會輿論模型”、“戰爭爆發模型”、“人的習慣模型”、“對策模型”、“攻擊與妥協模型”等等。突變理論能解說和預測自然界和社會上的突然現象，無疑它也是軟科學研究的重要方法和得力工具之一。

突變論在數學、物理學、化學、生物學、工程技術、社會科學等方面有著廣闊的應用前景。《大英百科年鑒》1977年版中寫道：“突變論使人類有了戰勝愚昧無知的珍奇武器，獲得了一種觀察宇宙萬物的深奧見解”。

自然，突變論的應用在某些方面還有待進一步的驗證，在將社會現象全部歸結為數學模型來模擬時還有許多技術細節要解決，在參量的選擇和設計模型方面還有大量工作要做。此外，突變理論本身也還有待於進一步完善，在突變論的方法上也有許多爭議之處。

總之，突變論問世以來，引起褒貶不一的評述，正象任何一門新興學科的發展經歷一樣。著名數學家斯圖爾特客觀地評價了突變論，他寫道：“適當地理解突變理論，可以為人們生存的世界提供新穎而深入的見解。但它還需要加以發展、檢驗、修改，經歷一般成為可靠的科學工具的全部過程。但我毫不懷疑，也不是宇宙中的唯一事物”。

突變理論在許多領域已經取得了重要的應用成果。隨著研究的深入，它的應用範圍在不斷擴大，相信它在中國建設中將發揮重要作用。

突變理論-圖示解析

突變理論20世紀70年代發展起來的一個新的數學學科。一種自然現象或一個技術過程，在發展變化過程中常常會從一個狀態跳躍式地變到另一個狀態，或者說經過一段時間緩慢的連續的變化之後，在一定的外界條件下，會產生一種不連續的變化，這就是所謂的突變現象。

這類突變現象在大自然里以及在技術過程中都是普遍存在的。例如，一定質量的氣體在一定的溫度和壓力之下會變成液體，天氣的突然變化會產生暴風雨，地殼的劇烈運動會引起地震，橋樑的扭曲會導致斷裂，容器里的幾種物質在一定的外界條件下會發生化學反應，胚胎的發育，等等，這些現象都是突變現象。

以前科學家們在研究這類突變現象時遇到了各式各樣的困難，其中主要困難之一就是缺乏恰當的數學工具來提供描述它們的數學模型。1969年法國數學家勒內·托姆在他的題為《生物學中的拓撲模型》一文中，首次在奇點分類的基礎上提出了一個描述突變現象的數學模型。稍後，他在著名的《結構穩定與形態發生》一書中又系統地闡述了他的思想，這就是現在人們所稱的突變理論。

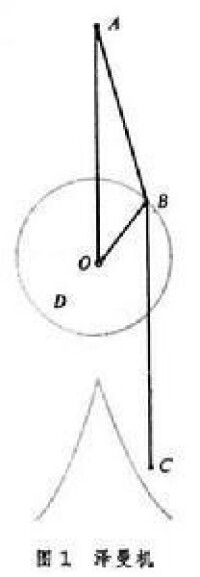
澤曼機是E.C.澤曼為闡述突變理論而構造的一個力學例子。D是一個半徑為1的圓盤，它可以圍繞xy平面的原點O自由轉動。A是xy平面上的一個固定點，AO的長為3,B是圓盤上的一個固定點，取兩條長度為1的彈性帶子，把其中的一條的一端固定在點A,另一端固定在圓盤上的點B處；另一條彈性帶子的一端固定在B處，另一端C在平面上自由移動。當點C在平面上連續變動時，只要BC的長度大於1，那麼在彈性力的作用下，一般說來，圓盤是跟著C點的移動而連續地轉動。

在實驗中發現，當C移動到某些點時，圓盤會從一個狀態跳躍到另一個狀態，發生了不連續的變化即突變。通過實驗就可以看到這種突變點構成一條如圖1 突變理論所示的尖點狀的曲線。對這樣一個力學系統的運動，取直線OA為y軸，首先找出刻畫圓盤狀態的參數，可以用OB與OA的夾角θ來刻畫圓盤的狀態並稱θ為狀態參數，或稱內參數。點C的運動控制著圓盤的運動，所以點C的坐標(x,y)就稱為控制參數或外參數。

由胡克定律可知，這個力學系統有個勢函數。當兩條彈性帶子的長度分別為l1、l2時，它們的總勢能為，式中，將

代入V,可以看出V是θ、x、y的函數。由極小勢能原理可知，當點C的坐標為 時，圓盤狀態 應使 為勢函數 的極小值。也就是說，這個力學系統的狀態 應滿足方程式。在三維空間 中，方程式確定一曲面，記作MV並稱它為狀態曲面或突變流形。它上面的點代表這個力學系統的一個狀態。從奇點理論研究的結果知道，可以選取適當的坐標 使得函數V在新坐標系中有很簡單的分析表達式：

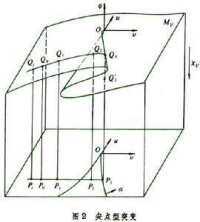
而狀態曲面MV由方程

所決定。這個曲面圖形如圖2所示。

幾何上曲面MV是這樣描述力學系統運動的：為了使圖看起來清晰，把u,υ平面沿φ軸向下平移一個距離，ⅩV表示MV到(u,υ)平面的垂直投影，曲面MV的兩條摺疊線在ⅩV下的像是一條尖點曲線α，給定一點，圓盤的狀態 應該使

,

即 是曲面MV上的一點 Q0，亦即通過點(u0，υ0)平行於φ軸的直線與MV的交點就是。當控制參數p=(u,υ)在平面上沿一條曲線從p0連續地變到p1,p2時，相應的代表系統狀態的點Q就從Q0連續地沿著曲面上一條曲線變到Q1,Q2。但當點p通過曲線上的點p3時，相應的代表系統狀態的點Q就從曲面的摺疊處（懸崖上）掉到曲面的下面一葉上的點Q3，這就是代表系統狀態的點Q產生了不連續的跳躍，即描述了系統的突變運動。

曲線α具有重要性質：當控制參數(u,υ)穿過它時，系統狀態產生突變。曲線α看作點集並稱為突變集，而ⅩV稱為突變映射。研究一下曲面MV和映射ⅩV:MV→ 就可以看到曲線α就是映射ⅩV的奇點集在ⅩV下的像。因此，若要找突變集，首先是要求出ⅩV的奇點集。

由這個力學的實例可以概括出研究突變現象的數學方法：

① 確定刻畫系統狀態的參數 及系統的控制參數。在上例中就是確定出刻畫圓盤的狀態的參數θ以及控制參數(x,y)。

② 確定支配系統的勢函數 在控制參數為 時系統的平衡態 使得勢函數p取極小值，在上例中就是找出系統的彈性勢能。

③ 確定系統所有可能出現的平衡態構成的空間Mp,Mp是 中由方程式

所確定的子流形。

④ 研究Mp到 上的投影 → ，以 記 的奇點集，中的 稱為分歧集。它確定了突變可能發生的範圍。一般說來，勢函數可以是非常複雜的。但是托姆關於基本突變分類定理告訴人們，儘管勢函數 p千千萬萬，但是只要勢函數的控制參數 的個數不超過4,用奇點的語言就是：的余維r≤4,結構穩定的勢函數的拓撲型（即在坐標的微分同胚變換之一）只有七種類型。