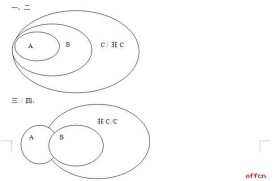
三段論推理
演繹推理中的一種
三段論推理是演繹推理中的一種簡單推理判斷。他包括:一個包含大項和中項的命題(大前提)、一個包含小項和中項的命題(小前提)以及一個包含小項和大項的命題(結論)三部分。三段論實際上是以一個一般性的原則(大前提)以及一個附屬於一般性的原則的特殊化陳述(小前提),由此引申出一個符合一般性原則的特殊化陳述(結論)的過程。三段論是人們進行數學證明、辦案、科學研究等思維時,能夠得到正確結論,的科學性思維方法之一。是演繹推理中的一種正確思維的形式。
定義
三段論推理是演繹推理中的一種簡單推理判斷。
它包含:一個一般性的原則(大前提),一個附屬於前面大前提的特殊化陳述(小前提),以及由此引申出的特殊化陳述符合一般性原則的結論。
三段論推理:思維時,大腦首先用一個人為定義的內容極為明確的、囊括的範圍比較大的總的原則A(簡稱‘大前提’),再通過科學實驗尋找另外一個概念小前提B,B的概念的全部內涵能夠一定被包含在大前提A內、並且用文字描述的B的概念的內容時,不能人為與大前提A的內容本質完全一樣(B簡稱小前提),然後按照小前提B如果屬於大前提A範圍內,那麼B的性質一定與大前提的性質一樣,而得到可靠而正確的判斷,此思維過程叫做正確的下結論C過程——科學術語叫做“三段論推理”。
註:由此‘三段論’方法判斷出的新結論,還可以成為人們下一步驚喜研究的新起點。‘三段論’思維,B必須有的堅實的‘論據’,否則得到的結論C就可以說是錯誤的。愛因斯坦的《相對論》C的得來也是依靠‘三段論推理’。凡是違背‘三段論’原則的思維都是不可能得到可靠的結論。容易導致‘循環論證’形式:例如“實踐是檢驗真理的唯一標準”人為把‘三段論’變為‘二段論’,錯誤在於,論題也就是論據,非法地合二而一了,自己證明自’成立在《邏輯學》中是非法的。
三段論是人們進行數學證明、辦案、科學研究等思維時,能夠得到正確結論,的科學性思維方法之一。是演繹推理中的一種正確思維的形式。
1、思維過程比喻:大桌子上有碗——全家的碗一定在桌子上——紅葡萄一定在碗里——紅葡萄一定在大桌子上,不需要開飛機滿世界尋找。
上面的三段論推理,“所有動物”是連接大、小前提的中項;“有些生物吃肉”是出現在大前提中又在結論中做謂項的“大項”;“老虎”是出現在小前提中又在結論中做主項的“小項”。(習慣上,不用ABC而用“P”表示“大項”,用“M”表示“中項”,用“S”表示“小項”。)
(1)省略了‘大前提’:
①你是經濟學院的學生,你應當學好經濟理論。
例①省略了大前提“凡是經濟學院的學生都應該學好經濟理論”。
②改革是新事物,當然免不了要遇到前進中的困難。
例②省略了大前提:“凡是新事物都免不了遇到前進中的困難”。
(2)省略了‘小前提’:
①企業都應該提高經濟效益,國營企業也不例外。
例①省略了小前提“國營企業也是企業”。恢復其完整式是:“企業都應該提高經濟效益,國營企業也是企業,所以,國營企業應該提高經濟效益”。
②這部連續劇不是優秀作品,因為優秀作品是思想性與藝術性相結合的作品。
例②省略的小前提是“這部連續劇不是思想性與藝術性相結合的作品”。恢復其完整式是“優秀作品都是思想性與藝術性相結合的作品,這部連續劇不是思想性與藝術性相結合的作品,所以這部連續劇不是優秀作品”。
(3)省略了結論:
①業餘辦學形式是群眾所歡迎的,函授教育就是一種業餘辦學形式。
例①省略的結論是“函授教育形式是群眾所歡迎的”。
②所有的人都免不了犯錯誤,你也是人嘛。
例②省略的結論是“你也免不了犯錯誤”。
註:*由此‘三段論’方法判斷出的新結論,還可以成為人們下一步繼續進行研究的新起點。‘三段論’思維,B必須有的堅實的‘論據’,否則得到的結論C就可以說是錯誤的。愛因斯坦的《相對論》C的得來也是依靠‘三段論推理’。
凡是違背‘三段論’原則的思維都是不可能得到可靠的結論。容易導致‘循環論證’形式:例如“實踐是檢驗真理的唯一標準”人為把‘三段論’變為‘二段論’,錯誤在於,論題也就是論據,非法地合二而一了,‘自己證明自己’成立在《邏輯學》中是非法的。
三段論:如果一類對象A的全部內涵可以知道,那麼,它的小類B,即A包含的部分對象B,也必然有A的全部內涵;我們想否定應該內容時:如果某一類對象A的全部都不是B,E如果屬於B,則E也必然不屬於A。也就是說,如果我們對某類對象A的全部,經過研究都有所斷定是否正確?那麼,對A包含的部分對象B也就可以斷定了(斷定B‘是’或者'不是')。
按照語言描述的順序決定的大項、小項、中項在三段論中不同的位置分佈,三段論可分為以下四個格:
| 第一格 | 第二格 | 第三格 | 第四格 | |
| 大前提 | M——P | P——M | M——P | P——M |
| 小前提 | S——M | S——M | M——S | M——S |
| 結論 | S——P | S——P | S——P | S——P |
可以看出,在這四個格中,結論中的主項和謂項的位置(在下面)是固定的。這些格的主要區別是,前提中的中項的位置不同。
同一格的三段論也有一定的差異,即它們的前提和結論中所涉及的直言命題的量詞(全稱、特稱)和質(肯定、否定)是不同的,也就是說它們的“式”是不同的。
例如:
1、所有的偶蹄目動物都是脊椎動物,牛是偶蹄目動物;所以牛都是脊椎動物。(第一格AAA式)
2、所有的偶蹄目動物都不是昆蟲,牛是偶蹄目動物;所以牛都不是昆蟲。(第一格EAE式)
3、所有商品都是用來交換的,所有封建地租都不是用來交換的;所以所有封建地租都不是商品。(第二格AEE式)
4、鴕鳥不會飛,鴕鳥是鳥;所以一些鳥不會飛。(第三格EAO式)
5、有些不會飛的動物是鴕鳥,鴕鳥是鳥;所以有的鳥是不會飛的動物。(第四格IAI式)
三段論的可能式和有效式:
在三段論的每格中,A、E、I、O四種判斷,都可以分別作為大、小前提和結論,其組合數量是:4X4X4=64。因此,就其可能性而言,每格有64個式。‘三段論’共有四個格,因此,三段論的可能式共有64X4=256個。
但是,三段論的可能式,並非都是有效的。事實上,其大部分是無效的。
對於三段論的所有可能式,都可以依據一般規則或各格的具體規則,判定它是否有效。經過篩選,三段論所有的可能式中,共有如下24個有效式:
| 第一格 | 第二格 | 第三格 | 第四格 |
| AAA | AEE | AAI | AAI |
| EAE | EAE | EAO | EAO |
| AII | AOO | AII | AEE |
| EIO | EIO | EIO | EIO |
| (AAI) | (AEO) | IAI | IAI |
| (EAO) | (EAO) | OAO | (AEO) |
驗證一個三段論正確的方法是:一個三段論是有效的,必須實現,當且僅當它是這個24個式中的一個。
上述24個有效式中,有5個帶括弧,稱為弱式。所謂弱式,是指‘本來可以得出全稱的結論,但卻只得出了特稱的結論。’可以不把弱式看成是獨立的有效式。
這樣,如果不算5個弱式,三段論共有19個‘有效式’。
三段論的各個有效式,我們不必要一個個地熟記。其實,判定三段論是否有效,你依據三段論的一般規則及各格的具體規則就可以正確判斷了。
三段論的省略式:
三段論包括大前提、小前提、結論三個部分。從邏輯結構上說,這三部分缺一不可。但是,三段論在日常語言的表達中,能常省略其中的某個部分。
在日常語言的表達中省略了大前提或者小前提或者結論的三段論,稱為三段論的省略式,也可以稱為‘省略三段論’。
‘省略三段論’所省略的描述性內容,只是語言表達而已,而不能省略其邏輯結構。也就是說,‘省略三段論’其所省略的部分,其實在邏輯結構上,被省略的仍是默認成為推理的必要部分,只不過人們沒有把它在語言上表達出來而已。(寫文章最好是不要省略,以免別人看不懂)。
省略三段論有三種形式:
第一,省略大前提:被省略的大前提,它的內容往往是人類已經獲得的普遍默認、承認的真理。(例如太陽從來東風升起;動物總是要死亡的)。
第二,省略小前提:省略的小前提往往是‘不言而喻的事實’。(堅實的證據)
第三,省略結論:省略的結論,(如果結論顯而易見,不容易誤解,有人認為不說出結論往往比說出結論‘更有力’。但是科學研究不允許含含糊糊。《邏輯學》思維下結論,不是文學作品。所以還是不省略結論,為好。
三段論省略式的恢復:
三段論省略式的必要性和長處,已如上述。
但三段論省略式也有弱點。一些前提虛假或推理錯誤的三段論,經省略后,很可能使這些毛病掩蓋起來,不易察覺。(詭辯者往往是有這些辦法搞理論上的渾水摸魚)。
因此,在判定‘省略三段論’的有效性時,就需要它們先把省略部分補充進去,把‘省略三段論’恢復成經典完整的形式。
‘省略三段論’的恢復,有以下步驟:
1,確定結論是否被省略?在下結論前,通常以“因此”、“所以”這樣的聯詞。根據是否有這樣的聯詞,你可容易斷定結論是否被省略了。
2,如果結論沒有被別人省略,那麼,根據結論,就可以確定大、小項。如果大項沒有在省略式的前提中出現,則說明省略的是大前提;如果小項沒有在前提中出現,則是省略的是小前提。
3,把省略的部分補充進去,並進行適當的整理,就可得到了‘省略三段論’的完整形式。
在恢復省略三段論時,要注意兩點:
第一,不可違反‘省略三段論’的原意。一般地說,‘省略三段論’的被省略部分的內容,是人們顯而易見的,才可以省略。要按照‘省略三段論’明顯的原意進行恢復。不能為‘避免省略三段論恢復后出現形式錯誤’而違反它的原意進行錯誤的恢復。
第二,如果對‘省略三段論’原意的理解存在岐義,那麼,你在恢復時所補充的判斷內容,應該力求是真實的。如果雖然不違背原意去補充一個真實的判斷作為前提或結論,卻錯誤地補充了一個虛假的判斷,這就失去了恢復‘省略三段論’的意義。是幫倒忙。
所謂‘推理的有效性’,就是通過推理,從真的前提出發思維(實事求是的內涵)非常重要,因為必然只能得到真的可靠的結論。如果一個推理形式是從‘真前提’推出假結論,那麼這個推理形式就是無效的。(簡稱“推不出”)但是人們有時不知道這是假的結論,以為這就是"真理"。
傳統邏輯中,三段論的256個式中有如下24個有效式,其它的式都是無效的。
第一格:AAA,EAE,AII,EIO;AAI,EAO。
第二格:AEE,EAE,AOO,EIO;AEO,EAO。
第三格:AII,IAI,OAO,EIO;AAI,EAO。
第四格:AEE,IAI,EIO;AEO,EAO,AAI。
注意:分號前是無條件有效式,分號后是有條件有效式,下面會講解。
傳統邏輯假定結論的主項(小項)不是空的,也就是說這一項所表達的集合的元素是存在的,這個假定保證了以上四個格中分號後面的9個式是有效的,分號前面15個式的有效性不受這個假定的影響。可以看到,分號后的9個有效式都有一個特點,那就是結論是特稱的,而前提都是全稱的。
按照布爾的觀點,全稱命題不蘊含存在,也就是說‘不能只用全稱命題推出特稱命題’(一般而言,特稱命題都被認為是有存在含義的,“有的A是B”的意思是“存在一個A且那個A是B”)。例如“所有汽車都是交通工具”不蘊含“汽車存在”的意思,所以他認為三段論只有分號前的15個有效式。
而亞里士多德認為在主項實際存在時全稱命題就蘊含存在,反之則不蘊含。例如“所有汽車都是交通工具”蘊含汽車存在,而“所有獨角獸都是只有一隻角的動物”不蘊含獨角獸存在,所以他認為在小項(即上面的“汽車”、“獨角獸)不空時,分號后的9個式也是有效的。我們也可以說,分號前的15個有效式是無條件有效的,后9個有效式是有條件有效的。
不難看出,第一格的有效式的結論含有AEIO四種形式,第二格只有否定的E、O兩種形式,第三格只有特稱的I、O兩種形式。第一格的有效式的結論既含有直言命題的全部形式,又比較符合日常表達習慣,所以它是比較重要的,後面我們可以看到,三段論的有效式都可以用第一格的前四個式證明。
一般規則如下:
(1)一個正確的三段論,有並且只有三個不同的項。
三段論的實質就是藉助於一個共同項即中項作為媒介,使大小項發生邏輯關係,從而導出結論的。如果一個三段論只有兩個詞項或四個詞項,那麼大小項就找不到一個聯繫的共同項,因而無從確定大小項之間的關係。因此,一個正確的三段論僅允許有三個不同的詞項。
如果僅有兩個詞項(A是B,所以B是A),就造成了無意義的同語反覆,(循環論證)不能推出新結論。也不能犯“四詞項”邏輯錯誤(a是b;c是d,所以a是d);
(2)三段論的中項至少要周延一次。(為了避免出現邏輯性錯誤)
中項是聯繫大小前提的媒介。如果中項在‘前提’中一次也沒有周延,那麼,中項在大、小前提中將會出現部分外延與大項相聯繫,並且部分外延與小項相聯繫,這樣大、小項的關係就無法確定。
中項不能在大、小前提中兩次不周延。若中項在大小前提中周延一次或周延兩次,情況又如何呢?如果中項周延一次,那麼就會有一個中項的全部外延和大項或小項發生了肯定或否定的關係,從而產生媒介作用,使大小前提發生聯繫推出必然結論。
正確思維的例子:
①知識分子B屬於勞動者A(更大的範圍),李教授T是知識分子B,所以李教授T屬於勞動者A。
②知識分子B不是剝削者Z,李教授T是知識分子B,所以李教授T不是剝削者。
③凡作案者D都有作案動機H,某人W沒有作案動機D;所以某人D不是作案動機者H。
上述例子都是僅有一個中項是周延的,它們都能推出必然結論,大小前提與結論的聯繫都是必然的。
如果中項周延兩次,只要大小前提不都是否定的,那麼,中項的全部外延就會分別與大項、小項發生聯繫,起到聯結大小項的作用,從而使三段論推出必然的結論。
綜上所述,一個正確的三段論(只要兩個前提不都是否定的),它的中項至少應周延一次。
(3)在前提中不周延的詞項,在結論中不得周延。
本條規則與性質判斷直接換位推理的規則相同。如果前提中的大項或小項是不周延的,那麼它們的大項或小項的外延就沒有被全部斷定,若結論中的大項或小項變為周延的,那麼就等於斷定了大項或小項的全部外延。這樣,造成了前後不一致,所推出的結論當然是不可靠的,其結論也不是由前提必然推出的。違反這條規則,所犯的邏輯錯誤稱為“大項不當擴大”或“小項不當擴大”。
例子:[注意,A的內涵大於B,例如A包括B、C、D、E、......]
①先進工作者B都是工作有成績A的人,老王不是先進工作者B,所以老王不是工作有成績的人。(錯)
②金屬B都是導電體A,橡膠不是金屬B,所以橡膠不是導電體A。(錯)
③金屬B都是導電體A,金屬B都不是絕緣體E,所以,所有絕緣體E都不是導電體。(對)
④某人A是教授B,某人A是北京大學C的,所以,北京大學的都是教授。(錯)(職位與位置概念不同)
上面的例子①②③所犯的邏輯錯誤都是“大項不當擴大”。例④所犯的邏輯錯誤是“小項不當擴大”。從上面的例子來看,結論有假有真,這說明違反本條規則所推出的結論是不可靠的,也就是說,從前提推出的結論不是必然得出的,而是或然的。我們不能因為有例②例③這種能夠推出真實結論的推理,就認為例②例③是有效性推理。能夠偶然推出真實結論的推理形式並非是有效的,凡是有效推理的邏輯形式,代入任何推理內容,只要前提真實,就一定能夠推出真實的結論。
(4)兩個否定前提不能推出結論。
如果兩個前提都是否定的,那麼中項同大小項發生排斥。這樣,中項就無法起到聯結大小前提的作用,小項同大項的關係也就無法確定,因而推不出結論。下面舉兩個例子說明該規則。
①銅(M)都不是絕緣體(P),而鐵(S)不是銅(M),所以鐵(S)不是絕緣體(P)。
②羊(M)不是肉食動物(P),而虎(S)不是羊(M),所以虎(S)不是肉食動物(P)。
上面兩例,前提都是真實的,但由於形式無效,所以推出的結論有或然性。
(5)前提有一個是否定的,其結論必是否定的;若結論是否定的,則前提必有一個是否定的。
該規則是導出規則。若一個三段論的大前提是否定的,那麼,中項與大項這兩者的外延就必然是互相排斥的,據規則(4)“兩個否定前提不能推出結論,這樣,小前提就只能是肯定的。若小前提是肯定的,那麼,小前提中的中項和小項的外延就必然具有相容關係。這樣,通過中項的媒介作用,小項就會與大項的外延相排斥,從而推出必然性結論。同理,若小前提是否定的,那麼,中項與小項的外延相排斥;據規則(4),大前提只能是肯定的,則中項與大項的外延就必然具有相容關係。
從另一個角度看,若前提都是肯定的,而結論是否定的,那麼,結論的小項和大項的關係,或是真包含關係,或是交叉關係,或是全異關係,而實際上大小肯定前提通過中項聯結,小項和大項的外延關係可能是全同關係,或真包含於關係,或真包含關係,或交叉關係,這樣在前提中蘊涵的小項與大項的關係同結論中的小項與大項的關係存在著差異,從而使結論失去可靠性,其邏輯形式也必然是無效的。
(6)兩個特稱前提推不出結論
如果兩個前提都是特稱判斷,對於三段論來說,共有四種組合情況。即II、OO、IO、OI。下面分別進行分析。
如果兩個前提是II式,則兩個前提中的主謂項均是不周延的。這樣,不論中項位於兩個前提的主項還是謂項,都不能夠周延,必然違反規則(2),其推理形式也是無效式。
如果兩個前提是OO式,則違反了規則(4)。因此其推理形式也是無效式。
如果兩個前提是IO式,則違反規則(3)。因為大項無論是I判斷的主項還是謂項,都不可能是周延的,而據規則(5)結論應是否定的,這樣結論的大項是周延的,從而就一定違反規則(3),其推理式也是無效式。
如果兩個前提是OI式,則或違反規則(2),或違反規則(3)。若中項是大前提O判斷的主項,同時小前提中的中項或是其主項或是謂項,則兩個中項在大小前提中都不周延,必然違反規則(2)。若大項P是大前提O判斷的主項,而據規則(5)結論必是否定的,這樣大項P在大前提中不周延而在結論中周延,就必然違反規則(3)。(以上理解時最好通過’桌子、碗、菜‘的關係尋找其容易理解的比喻方式去判斷)
所以,大小前提若都是特稱的,(理解,概念包含範圍過於小就不能演繹)則必然是無效式。
(7)前提中有一個是特稱的,結論必須也是特稱的。
根據規則(6),兩個特稱前提推不出結論,所以,一個正確三段論,前提若有一個是特稱,則另一個前提就必然是全稱的。這樣有一個前提是特稱的三段論,其大小前提的組合則有四種類型八種形式:
AI--IAAO--OAEI--IEEO--OE
上述四組中的“EO--OE”因兩個前提都是否定的,違反規則(4),所以該組可以直接排除,這樣,可分析的就剩下三組。
如果大小前提由AO組成,不管它們誰是大小前提,那麼它們的周延項有A判斷的主項和O判斷的謂項。根據規則(5),結論只能是否定判斷,若結論是否定判斷,則大項在結論中是周延的,為了遵守規則(3),大項只能在A判斷主項或O判斷的謂項的位置上,為了遵守規則(2),中項也只能在A判斷主項或O判斷的謂項的位置上,這樣,小項只能在不周延的項即A判斷的謂項或O判斷的主項的位置上,若結論的小項是全稱的,就必然違反規則(3),所以結論的小項只能是特稱的。
如果大小前提是IE,那麼,由於大前提I主謂項都不周延,而根據規則(5),其結論又只能是否定判斷,即大項在結論中是周延的,這樣只要大項在I判斷主項或謂項的位置上,就必然違反規則(3),所以IE為前提不能成立。若大小前提是EI,那麼其周延項有E判斷主項和謂項,為了不違反規則(2),保證中項周延一次,為了不違反規則(3),保證大項在結論中不擴大,小項只能位於I判斷主項或謂項,這樣,若結論的小項是周延的就必違反規則(3)。所以以EI為前提,其結論也只能是特稱判斷。
韋恩圖法是判斷三段論有效性的最終的也是最直接的方法。如圖所示,我們用三個圓來代表大項、小項和中項。中項所代表的集合是最上方的圓,大項是右下角的圓,小項是左下角的圓。畫這些圓時,應當確保圖中的7個區域被明顯的區分。
為了判定一個三段論的有效性,我們要先從語義中理解概念範圍,提取推理形式,然後將前提按一定順序輸入圖中,最後檢查結論是否正確,為了正確的輸入前提,需要遵照一定的規則:
1、所謂蔭蔽,指的是被蔭蔽的區域內不含任何元素,一般用斜線或陰影表示。
2、畫“X”表示所畫的區域中至少存在一個元素。
3、全稱的前提先輸入,特稱的前提后輸入。如果兩個前提都是全稱的,先輸入哪一個都可以。
4、要畫x的區域一般都被分為兩部分,若有一個部分被蔭蔽,x要畫在未被蔭蔽的部分。若沒有區域被蔭蔽,x要畫在兩個區域的交線上。
還要注意以下幾點:
1、所有標記(畫x或蔭蔽)都是對前提而言,沒有標記,是為下結論所做。
2、輸入’前提‘時只需關注該前提所涉及的兩個詞項的圓,另一個圓只需極小的關注。
3、蔭蔽區域時一定要蔭蔽相關區域的“全部”。
4、特稱結論“有的S是P”的含義是:至少存在一個S並且這個S是P。“有的S不是P”也一樣。
5、未被標記的區域的情況是未知的,可能存在元素也可能不存元素,要根據實際情況而定。
另外一點,對於分號前和分號后的式子,驗證方法略有不同。
讀者可以在下面的例子中再仔細體會。
例一,驗證第一格AAA式即“所有M是P,所有S是M,所以所有S是P”的有效性,如圖所示。
第二步:因為“所有”S都屬於M,所以’只屬於S而不屬於M的事物是不存在的‘,所以我們就將區域5和6蔭蔽。
第三步:檢查結論,發現S只剩下區域3,而區域3中的元素也必定屬於P,所以結論“所有S是P”成立。
第四步:得出結論,該三段論是有效的。
例二,驗證第三格IAI式即“有的M是P,所有M是S,所以有的S是P”的有效性,如圖所示。
第二步:再輸入特稱的前提“有的M是P”,這句話意味著在M和P的共有區域或者說交集中至少有一個元素,即區域3、4的並集中至少存在一個元素,但4已被蔭蔽,所以將x畫在區域3中。
第三步:檢查結論,“有的S是P”說明S和P的交集中即區域3、6的並集中至少有一個元素,而x恰好在區域3中,結論成立。
第四步:得出結論,該三段論是有效的。
再來看一個分號后的例子。
例三,證明第一格EAO式即“所有M都不是P,所有S都是M,所以有的S不是P”,如圖所示。
第二步:輸入“所有S都是M”,蔭蔽區域5、6。
第三步:檢查結論,“有的S不是P”意味著存在一個x並且那個x是S而不是P,即區域2、5的並集中存在一個x,檢查圖形卻沒有這個x。因此該三段論按布爾的觀點是無效的,我們繼續論證該三段論在亞里士多德的觀點下是有效的。
第四步,檢查有無只剩一個區域沒有被蔭蔽的圓,若沒有則該三段論是無效的。發現S只剩一個區域2未被蔭蔽,因此在區域2中畫上一個帶圓圈的叉。
第五步,再次檢查結論,得到了所需的x。這時,若S是現實存在的項,三段論就是有效的,若S不是現實存在的項,例如“當今存活的霸王龍”等等,那麼三段論就是無效的。
注意,有時會出現一個以上的只剩一個區域沒有被蔭蔽的圓,這時只需將帶圈的x畫在S的範圍內就可以了。第二格的AEO式和EAO式就是如此。
最後再舉一個被證明為無效的例子。
例四,驗證第一格IAI式即“有的M是P,所有S是M,所以有的S是P”的有效性。
如圖所示。
第一步:先輸入全稱的前提“所有S是M”,蔭蔽區域5、6。
第二步:再輸入特稱的前提“有的M是P”,即區域3、4的並集中存在一個x,但這兩個區域都未被蔭蔽,所以將x畫在區域3、4的交線上。
第三步:檢查結論,“有的S是P”說明S和P的交集中至少存在一個x,即區域3、6的並集中存在一個x,但我們所畫的x卻不知道到底是在區域3中還是區域4中,兩者都有可能。所以當x在區域4中時,前提真而結論假。同時又找不到只剩一個區域未被蔭蔽的圓,因此該三段論是無效的。
最後給出24個有效式的韋恩圖證明,如圖所示。
除了運用韋恩圖法,也可以通過運用一些規則,將欲證的三段論化為第一格分號前的四個有效式,從而證明三段論的有效性。
規則:(為了輸入方便,否定用“~”表示)。
規則Ⅰ1:MAP,SAM,|-SAP(“|-”表示“必然地得出”)。
規則Ⅰ2:MEP,SAM,|-SEP。
規則Ⅰ3:MAP,SIM,|-SIP。
規則Ⅰ4:MEP,SIM,|-SOP。
換位規則:SEP,|-PES。
換位規則:SIP,|-PIS。
差等規則:SAP,|-SIP。
差等規則:SEP,|-SOP。
矛盾規則:SAP,|-~(SOP)。
矛盾規則:SEP,|-~(SIP)。
前四個規則是第一格分號前的四個有效式,後面的規則是和直言命題有關的規則。
例一:證明第二格AEE式
∴SEP
1)PAM前提。
2)SEM前提。
3)MES2),換位規則[這種寫法是說“對2)使用換位規則”,下同]。
4)PES3),1),Ⅰ2。
5)SEP4),換位規則。
這就得到了所需的結論。
例二:證明第一格EAO式
∴SOP
1)MEP前提。
2)SAM前提。
3)SEP1),2),Ⅰ2。
4)SOP3),差等規則(使用差等規則證明的都是分號后的有效式,要確保S項的存在性)。
運用形式證明,可以將欲證的三段論化為第一格的前四個有效式,這種證明方法叫做三段論還原法。
備註:為了正確的運用三段論,必須要判斷它的有效性,人們記住全部24種有效形式是比較困難的,可以利用多種方式,證明三段論的有效性。