直言命題
性質命題
直言命題亦稱“定言命題”。即性質命題。由於在性質命題中,對對象具有或不具有某種性質的斷定是直接的、無條件的,因而,邏輯史上把這種命題稱為直言命題,以別於假言命題(對對象的某種斷定是有條件的)和選言命題(對對象的某種斷定是有選擇的)。
把命題分為直言命題、假言命題和選言命題,是從康德開始的。
邏輯史上最早詳細研究這類命題的是亞里士多德,但他並沒有使用“直言命題”這個名稱,而稱之為簡單命題。後來,康德從認識的模態的角度把這類命題叫做實然(原意為斷言)命題。傳統邏輯學家一般認為,這類命題與選言命題、假言命題不同,它是無條件地、簡單地肯定或否定某種事實,因而被漢譯為直言命題。
概念:判定(區別、識別)對象。
按照不同的標準,直言命題可以分為不同的種類。
| 名稱 | 表達 | 縮寫 | 簡稱 |
| 全稱肯定命題 | 所有的S是P | SAP | A命題 |
| 全稱否定命題 | 所有的S不是P | SEP | E命題 |
| 特稱肯定命題 | 有的S是P | SIP | I命題 |
| 特稱否定命題 | 有的S不是P | SOP | O命題 |
按命題的量劃分,直言命題可分為單稱命題、全稱命題、特稱命題。
按命題的質劃分,直言命題可分為肯定命題、否定命題。
按命題的質與量劃分,直言命題可分為單稱肯定命題、單稱否定命題、全稱肯定命題(SAP)、全稱否定命題(SEP)、特稱肯定命題(SIP)、特稱否定命題(SOP)。
單稱命題是直言命題中的一類特殊形式,可分為兩種:一種是主項是專名,如“蘇格拉底是人”;另一種是主項是附有限制的普遍概念,如“昨天我談到的那個人是作家”。單稱命題有肯定和否定的區別,傳統邏輯認為其形式分別為:這個S是P;這個S不是P。亞里士多德雖論及單稱命題,但卻沒有談到有關單稱命題的推理。後來許多傳統邏輯讀本在論述推理時,由於單稱命題和全稱命題都是判定一個主項外延的的全部,所以常把單稱命題劃歸到全稱命題,因此,六種命題就成為四種類型。
全稱肯定命題反映了主項的所有外延全都具有某種性質,表示形式為:所有S是P,縮寫為SAP,簡稱A命題。
全稱否定命題反映了主項的所有外延全都不具有某種性質,表示形式為:所有S不是P,縮寫為SEP,簡稱E命題。
特稱肯定命題反映了主項的一部分外延都具有某種性質,表示形式為:有的S是P,縮寫為SIP,簡稱I命題。
特稱否定命題反映了主項的一部分外延全都不具有某種性質,表示形式為:有的S不是P,縮寫為SOP,簡稱O命題。
直言命題一般由主項、謂項、質(聯項)、量項四部分構成。
主項是指直言命題中指稱事物的詞。
謂項是指直言命題中指稱事物所具有或不具有的性質的詞項。
聯項又稱為直言命題的質,是表示主項與謂項之間邏輯關係的詞項。聯項有肯定的與否定的兩種。肯定聯項一般用語詞"是"表示;否定聯項一般用語詞"不是"表示。
周延情況不同故稱量
量項又稱為直言命題的量,是表示主項外延數量的詞項。量項有全稱量項和特稱量項兩種。全稱量項一般用語詞"所有",“任何”,"每一個",“一切”等表示;特稱量項一般用"有的","一些",“存在”,“至少有一個”等表示。
周延性的定義:在性質命題中,對主、謂項外延數量的斷定情況。即:周延性是針對“項”而言的。
在直言命題的這四個組成部分中,量項和聯項的邏輯涵義是確定的,邏輯涵義確定的詞項被稱作邏輯常項。因此,直言命題的量項和聯項是邏輯常項。
與量項和聯項不同,主項和謂項的邏輯涵義是不確定。邏輯涵義不確定的詞項被稱作邏輯變項。因此,主項和謂項是變項,分別用S和P表示。
雖然就主項S和謂項P究竟代表哪個具體詞項來說它們的涵義是不確定的,但就它們必須代表並且也只能代表詞項這一點卻是很確定的。因此,我們說S和P是以詞項為定義域的變項,它們代表任意詞項,而不是其它什麼東西。
直言命題的一般結構為:量項+主項+聯項+謂項。也可以表示為:所有(有的)S是(不是)P。
主項、謂項相同的A、E、I、O四種命題之間存在著一定的真假制約關係。在邏輯學上,這種真假制約關係稱為對當關係。A、E、I、O四種命題有以下的對當關係。
| 命題類型 | 命題間的真假關係 | ||||
| 全同 | 下屬 | 上屬 | 交叉 | 全異 | |
| A命題 | 真 | 真 | 假 | 假 | 假 |
| E命題 | 假 | 假 | 假 | 假 | 真 |
| I命題 | 真 | 真 | 真 | 真 | 假 |
| O命題 | 假 | 假 | 真 | 真 | 真 |
A命題與E命題之間存在反對關係。反對關係的特徵是:一個命題真,另一個命題必假;一個命題假,另一個命題不能確定真假,即:二者可以同假,但不能同真。
在A、E兩個判斷中,如果我們知道其中一個是真的,就可推知另一個是假的。例如:
已知A:所有事物都是運動的(真)則E:所有事物都不是運動的(假)
已知E:所有的科學家都不是思想懶漢(真)則A:所有的科學家都是思想懶漢(假)
如果我們知道其中一個是假的,那麼另一個真假不定。例如:
已知A:我班同學都學過日語(假)則E:我班同學都沒學過日語(真假不定)
I命題與O命題存在下反對關係。下反對關係的特徵是:一個命題真,另一個命題不能確定真假;一個命題假,另一個命題必真,即:二者可以同真,但不能同假。
在I、O兩個判斷中,如果我們知道其中一個是假的,那就可以斷定另一個是真的。例如:
已知O:有些事物不是運動的(假)則I:有些事物是運動的(真)
如果我們知道其中一個是真的,那麼另一個真假不定。例如:
已知I:我班有些同學學過日語(真)則O:我班有些同學沒學過日語(真假不定)
A命題與O命題,E命題與I命題之間存在矛盾關係。矛盾關係的特徵是:一個命題真,另一個命題必假;一個命題假,另一個命題必真,即:二者不能同假,也不能同真。
A:所有事物都是運動的(真)O:有些事物不是運動的(假)
O:有些工商幹部不是大學畢業生(真)A:所有的工商幹部都是大學畢業生(假)
I:有些物體是固體(真)E:所有物體都不是固體(假)
E:語言都不是上層建築(真)I:有些語言是上層建築(假)
A命題與I命題,E命題與O命題之間存在差等關係。差等關係的特徵是:全稱命題真,特稱命題必真;特稱命題真,全稱命題真假不定;全稱命題假,特稱命題不能確定真假;特稱命題假,全稱命題必假。
例如:
已知A:所有事物都是運動的(真)則I:有些事物是運動的(真)
已知I:有的單位參加了義務獻血。(假)則A:所有的單位都參加了義務獻血(假)
已知A:我班同學都學過日語(假)則I:我班有些同學學過日語(真假不定)
已知I:我班有些同學學過日語(真)則A:我班同學都學過日語(真假不定)
類似地,可舉例說明E和O判斷之間的差等關係
為了便於記憶,邏輯學中把A、E、I、O四種判斷之間的關係用下列"邏輯方陣"來表示:
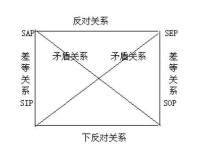
直言命題
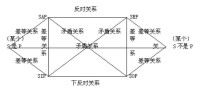
直言命題
直言命題的對當關係推理是指根據命題的四種對當關係得出結論的推理。直言命題有四種對當關係,相應地,直言命題有四種對當關係的推理。如下表所示:
| 對當關係推理 | 有效式 | 註釋 | |
| 反對推理 | SAP→¬SEP | SEP→¬SAP | ¬表示對一個命題的否定, →表示推出 |
| 下反對推理 | ¬SIP→SOP | ¬SOP→SIP | |
| 矛盾推理 | SAP→¬SOP | SOP→¬SAP | |
| ¬SAP→SOP | ¬SOP→SAP | ||
| SEP→¬SIP | SIP→¬SEP | ||
| ¬SEP→SIP | ¬SIP→SEP | ||
| 差等推理 | SAP→SIP | ¬SIP→¬SAP | |
| SEP→SOP | ¬SOP→¬SEP | ||
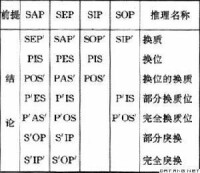
直言命題
換質法
通過改變作為前提的直言命題的聯項,從而得出另一個直言命題作為結論的推理方法。
規則:
1.改變前提的聯項,肯定變為否定,否定變為肯定;
2.把前提的謂項改為原詞項的負詞項,作為結論的謂項。
3.在結論中保留前提的主項和量項。
例子:
所有的金屬是導體,所以,所有的金屬不是非導體。
換位法
通過互換作為前提的直言命題的主項與謂項的位置,從而得出另一個直言命題作為結論的推理方法。
規則:
1.把前提的主項與謂項位置互換,作為結論的主項與謂項;
2.不得改變前提的聯項;
3.前提中不周延的詞項,在結論中也不得周延。
例子:
金屬是導體,所以,有的導體是金屬。
A、E、I、O命題都可以進行換質推理,在進行換質推理時要注意結論的謂項只能是與前提的謂項具有矛盾關係的詞項,而不能是與前提的謂項具有反對關係的詞項,否則這一換質推理是無效的。
與換質推理不同,只有A、E、I命題能進行換位推理,O命題不能進行換位推理,這是因為O命題的主項是不周延的,如果換位,那麼前提中不周延的主項作為結論中的謂項就會變得周延,這違反了換位法的規則,所以O命題的換位推理是無效的。同理,SAP換位后不能得到PAS,因為P在SAP中是不周延的,而在PAS中是周延的,也違反了換位法的規則,所以,該推理是無效的。
另外,換質法和換位法可以結合使用,通過對前提的既換質又換位,得出新的結論。在結合兩種方法使用時,既要遵守換質法的規則,也要遵守換位法的
現代邏輯克服了傳統邏輯不考慮空類和全類,即在S類和P類都既不空又不全的假設下討論A、E、I、O這四種直言命題的局限。現代邏輯考慮到詞項的外延可以是空類和全類,因而全稱命題如“凡未接觸過細菌的人都不得細菌性傳染病”的形式應該為(F(x)→G(x)),這可以讀作“對論域里的所有個體x而言,如果x有性質F則x有性質G”;而傳統邏輯所謂的特稱命題如“有金屬是固體”的形式應為('x(F(x))∧G(x)),這可讀作“在論域里至少存在一個體x,使得x有性質F並且x有性質G”。故現代邏輯稱這類命題為存在命題。
