玻璃化溫度

1、利用體積變化的方法

2、利用熱力學性質變化的方法

3、利用力學性質變化的方法

4、利用電磁性質變化的方法

玻璃化轉變溫度Tg是材料的一個重要特性參數，材料的許多特性都在玻璃化轉變溫度附近發生急劇的變化。以玻璃為例，在玻璃化轉變溫度，由於玻璃的結構發生變化，玻璃的許多物理性能如熱容、密度、熱膨脹係數、電導率等都在該溫度範圍發生急劇變化。根據玻璃化轉變溫度可以準確制定玻璃的熱處理溫度制度。對高聚物而言，它是高聚物從玻璃態轉變為高彈態的溫度，在玻璃化轉變溫度時，高聚物的比熱容、熱膨脹係數、粘度、折光率、自由體積以及彈性模量等都要發生一個突變。

從分子結構上講，玻璃化轉變溫度是高聚物無定形部分從凍結狀態到解凍狀態的一種鬆弛現象，而不像相轉變那樣有相變熱，所以它是一種二級相變(高分子動態力學中稱主轉變)。在玻璃化轉變溫度以下，高聚物處於玻璃態，分子鏈和鏈段都不能運動，只是構成分子的原子(或基團)在其平衡位置作振動；而在玻璃化轉變溫度時分子鏈雖不能移動，但是鏈段開始運動，表現出高彈性質，溫度再升高，就使整個分子鏈運動而表現出粘流性質。

在膨脹計內裝入適量的受測聚合物，通過抽真空的方法在負壓下將對受測聚合物沒有溶解作用的惰性液體充入膨脹計內，然後在油浴中以一定的升溫速率對膨脹計加熱，記錄惰性液體柱高度隨溫度的變化。由於高分子聚合物在玻璃化溫度前後體積的突變，因此惰性液體柱高度-溫度曲線上對應有折點。折點對應的溫度即為受測聚合物的玻璃化溫度。

利用高分子聚合物在玻璃化轉變溫度前後折光率的變化，找出導致這種變化的玻璃化轉變溫度。

（溫度-變形法）在加熱爐或環境箱內對高分子聚合物的試樣施加恆定載荷；記錄不同溫度下的溫度-變形曲線。類似於膨脹計法，找出曲線上的折點所對應的溫度，即為：玻璃化轉變溫度。

（DSC）以玻璃化溫度為界，高分子聚合物的物理性質隨高分子鏈段運動自由度的變化而呈現顯著的變化，其中，熱容的變化使熱分析方法成為測定高分子材料玻璃化溫度的一種有效手段。目前用於玻璃化溫度測定的熱分析方法主要為差熱分析（DTA和差示掃描量熱分析法（DSC）。以DSC為例，當溫度逐漸升高，通過高分子聚合物的玻璃化轉變溫度時，DSC曲線上的基線向吸熱方向移動（見圖）。圖中A點是開始偏離基線的點。將轉變前後的基線延長，兩線之間的垂直距離為階差ΔJ，在ΔJ/2處可以找到C點，C點所對應的溫度值即為玻璃化轉變溫度Tg。

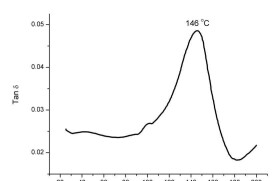
動態力學性能分析（DMA）法高分子材料的動態性能分析（DMA）通過在受測高分子聚合物上施加正弦交變載荷獲取聚合物材料的動態力學響應。對於彈性材料（材料無粘彈性質），動態載荷與其引起的變形之間無相位差（ε=σ0sin(ωt)/E）。當材料具有粘彈性質時，材料的變形滯後於施加的載荷，載荷與變形之間出現相位差δ：ε=σ0sin(ωt+δ)/E。將含相位角的應力應變關係按三角函數關係展開，定義出對應與彈性性質的儲能模量G’=Ecos（δ）和對應於粘彈性的損耗模量G”=Esin（δ）E因此稱為絕對模量E=sqrt(G’2+G”2)由於相位角差δ的存在，外部載荷在對粘彈性材料載入時出現能量的損耗。粘彈性材料的這一性質成為其對於外力的阻尼。阻尼係數γ=tan（δ）=G’’/G’由此可見，高分子聚合物的粘彈性大小體現在應變滯后相位角上。當溫度由低向高發展並通過玻璃化轉變溫度時，材料內部高分子的結構形態發生變化，與分子結構形態相關的粘彈性隨之的變化。這一變化同時反映在儲能模量，損耗模量和阻尼係數上。下圖是聚乙醯胺的DMA曲線。振動頻率為1Hz。在-60和-30°C之間，貯能模量的下降，阻尼係數的峰值對應著材料內部結構的變化。相應的溫度即為玻璃化轉變溫度Tg。

核磁共振法（NMR）溫度升高后，分子運動加快，質子環境被平均化（處於高能量的帶磁矩質子與處於低能量的的帶磁矩質子在數量上開始接近；N-/N+=exp(-E/kT)），共振譜線變窄。到玻璃化轉變溫度，Tg時譜線的寬度有很大的改變。利用這一現象，可以用核磁共振儀，通過分析其譜線的方法獲取高分子材料的玻璃化轉變溫度。