共找到18條詞條名為平行線的結果 展開
平行線
數學概念
幾何中，在同一平面內，永不相交（也永不重合）的兩條直線(line)叫做平行線（parallel lines）。
平行線公理是幾何中的重要概念。歐氏幾何的平行公理，可以等價的陳述為“過直線外一點有唯一的一條直線和已知直線平行”。而其否定形式“過直線外一點沒有和已知直線平行的直線”或“過直線外一點至少有兩條直線和已知直線平行”，則可以作為歐氏幾何平行公理的替代，而演繹出獨立於歐氏幾何的非歐幾何。
如果兩條直線都與第三條直線平行，那麼這兩條直線也互相平行。如若a∥b，b∥c，則a∥c。
在同一平面內，永不相交的兩條直線叫做平行線。平行線一定要在同一平面內定義，不適用於立體幾何，比如異面直線，不相交，也不平行。
在高等數學中的平行線的定義是相交於無限遠的兩條直線為平行線，因為理論上是沒有絕對的平行的。
平行線的定義包括三個基本特徵：一是在同一平面內，二是兩條直線，三是不相交。
在同一平面內，兩條直線的位置關係只有兩種：平行和相交。
平行線
平行線的性質與平行線的判定不同，平行線的判定是由角的數量關係來確定線的位置關係，而平行線的性質則是由線的位置關係來確定角的數量關係，平行線的性質與判定是因果倒置的兩種命題。對平行線的判定而言，兩直線平行是結論,而對平行線的性質而言，兩直線平行卻是條件。已知兩直線平行。由平行線得到角的關係是平行線的性質，包括：①兩直線平行，同位角相等；②兩直線平行，內錯角相等；③兩直線平行，同旁內角互補。
平行線的平行公理
1.經過直線外一點，有且只有一條直線與已知直線平行。
2.兩條平行線被第三條直線所截，同位角相等，內錯角相等，同旁內角互補。
注意：只有兩條平行線被第三條直線所截，同位角才會相等，內錯角相等同旁內角互補
平行線的判定
1、同位角相等，兩直線平行。
2、內錯角相等，兩直線平行。
3、同旁內角互補，兩直線平行。
4、在同一平面內，垂直於同一直線的兩條直線互相平行。
5、在同一平面內，平行於同一直線的兩條直線互相平行。
6、同一平面內永不相交的兩直線互相平行。
在歐幾里得幾何原本的體系中，這幾條判定法則不依賴於第五公設（平行公理），所以在非歐幾何中也成立。
找同位角 內錯角 同旁內角的方法
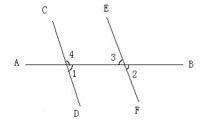
圖1，CD∥EF
如圖1，∠1與∠2是一組同位角，形成F型。
如圖1，∠1與∠3是一組內錯角，形成Z型。
如圖1，∠4於∠3是一組同旁內角，形成U型。
注意：只有題目已知有兩線互相平行才能證明它們是以上三個角的其中一個角。
平行線
“在平面內，如果兩條直線被第三條直線所截，一側的同旁內角之和大於兩個直角，那麼最初的兩條直線相交於這對同旁內角的另一側。”
這條公理的陳述過於冗長。在1795年，蘇格蘭數學家Playfair提出了以下以下公理作為平行公理的代替，在被人們廣泛的使用。
Playfair's Postulate:在同一平面內，過直線外一點，有且只有一條直線與這條直線互相平行。
平行公理的推論：（平行線的傳遞性）如果兩條直線都和第三條直線平行，那麼這兩條直線也互相平行。可以簡稱為：平行於同一條直線的兩條直線互相平行。
非歐幾何
由於平行公理陳述冗長，並且不像歐氏幾何中的其他公理那麼顯而易見，人們覺得它更像一個定理，可以從其他公理出發來證明。經歷了許多錯誤的證明，數學家們意識到這確實應作為一條公理。
更重要的是，在19世紀，數學家高斯，鮑耶，羅巴切夫斯基等發現，如果以平行公理的否定形式來代替平行公理，那麼可以演繹出一套和歐氏幾何完全不同，卻沒有內在矛盾的公理體系。這個大膽的觀點最初很難被人接受，但在邏輯上卻沒有任何問題。這個觀點成為人們對空間和幾何的認識的重大轉折點，包括愛因斯坦的廣義相對論，本質上都受到了這種觀點的影響。
在高等數學中的平行線的定義是相交於無限遠的兩條直線為平行線，因為理論上是沒有絕對的平行的。
在歐氏幾何中，在兩條平行線中做一條直線AB，以直線AB為半徑以逆時針方向做圓，然後以直線AB為半徑以順時針方向再做一個圓，從兩個圓的交點做垂線CD垂直於直線AB，若CD與AB的角的角度是90度，則說明兩條平行線不會相交。
但歐幾里得不敢思考當兩條平行線無限長時的情況。
於是包括羅素、黎曼在內的科學家假設當兩條平行線無限長時，他們會在無窮遠處相交。（例如：在地球的球面上，就會發現，相互垂直於赤道的經線會相交於北極點和南極點。）後來，非歐幾何和黎曼空間就誕生了，該成果給了愛因斯坦很大的啟發．
平行線公理就是區分歐氏幾何與非歐幾何的一個重要區別。
基本信息
- 中文名
- 平行線
- 外文名
- parallel line，parallel
- 屬性
- 平面幾何基礎，幾何線段
- 學科
- 數學