直角三角形斜邊中線定理
數學中關於直角三角形的定理
直角三角形斜邊中線定理是數學中關於直角三角形的一個定理,具體內容為:如果一個三角形是直角三角形,那麼這個三角形斜邊上的中線等於斜邊的一半。
:角形角角形,角形 斜邊的中線等於斜邊的一半。
逆題:角形線半,角形角角形,且角角形斜。
逆題確。該圓,線半徑圓,則該圓徑,該角形另頂圓,該頂角圓周角。徑圓周角角,逆題。
原命題2:如果CD是直角三角形ABC斜邊AB上的中線,那麼它等於AB的一半。
逆命題2:如果線段BD的一端B是直角三角形ABC的頂點,另一端D在斜邊AC上,且BD等於AC的一半,那麼BD是斜邊AC的中線。
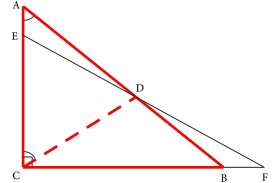
逆命題2是不成立的。舉一個反例。設直角三角形三邊長分別為AB=3,BC=4,AC=5。斜邊的一半長為2.5,斜邊上的高BE=(3*4)/5=2.4,在線段AE上上必能找到一點D,使BD=2.5,但BD並不是AC邊的中線,因為AC邊的中點在線段EC上。
直角三角形斜邊中線定理
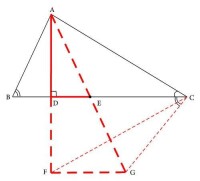
逆命題3:若直角三角形斜邊上一點與直角頂點的連線等於該點分斜邊所得兩條線段中任意一條時,該點為斜邊中點。幾何描述:在Rt△ABC中,∠ACB=90°,D是斜邊AB上一點。若CD=AD或CD=BD,則D是AB中點。
逆命題3成立,CD=AD則∠A=∠ACD,而∠A+∠B=90°,∠ACD+∠BCD=90°,因此∠BCD=∠B。等角對等邊,有CD=DB,所以AD=BD,即D是斜邊中點。
證法1:
ΔABC是直角三角形,作AB的垂直平分線n交BC於D
∴ AD=BD(線段垂直平分線上的點到這條線段兩端點的距離相等)
以DB為半徑,D為圓心畫弧,與BC在D的另一側交於C'
∴DC’=AD=BD∴∠BAD=∠ABD ∠C’AD=∠AC’D (等邊對等角)
又∵∠BAD+∠ABD+∠C’AD+∠AC’D =180°(三角形內角和定理)
∴∠BAD+∠C’AD=90° 即:∠BAC’=90°
又∵∠BAC=90°
∴∠BAC=∠BAC’
∴C與C’在直線AC上
又∵C與C’在直線BD上,AC與BD相交
∴C與C’重合(也可用垂直公理證明:假使C與C’不重合 由於CA⊥AB,C’A⊥AB 故過A有CA、C’A兩條直線與AB垂直 這就與垂直公理矛盾 ∴假設不成立 ∴C與C’重合)
∴DC=AD=BD∴AD是BC上的中線且AD=BC/2這就是直角三角形斜邊上的中線定理
證法2:
ΔABC是直角三角形,AD是BC上的中線,作AB的中點E,連接DE
∴BD=CB/2,DE是ΔABC的中位線
∴DE‖AC(三角形的中位線平行於第三邊)
∴∠DEB=∠CAB=90°(兩直線平行,同位角相等)
∴DE⊥AB
∴DE是AB的垂直平分線
∴AD=BD(線段垂直平分線上的點到這條線段兩端點的距離相等)
∴AD=CB/2
證法3:運用向量證明
已知Rt△ABC中,∠BAC=90°,AD是中線。求證BC=2AD
證明:設向量AC= b,向量AB= c,向量BC= a,向量AD= d
∵AD是BC的中線
∴ c+ b=2 d
∴( c+ b)²=4 d²
展開括弧,得| c|²+2 c· b+| b|²=4| d|²
又∵ c⊥ b
∴ c· b=0,| c|²+| b|²=| a|²
∴得| a|²=4| d|²
開方得| a|=2| d|,即BC=2AD
證法4:運用矩形的性質證明
延長AD到E,使DE=AD,連接BE,CE
∵BD=CD,∠BAC=90°
∴四邊形ABEC是矩形
∴BC=AE=2AD
證法5:解析幾何證明
以A為原點,AC為x軸,AB為y軸建立直角坐標系,並設C(2c,0),B(0,2b),那麼D(c,b)
|AD|=根號下C²+B²
|BC|=根號下(2C)²+(2B)² =2根號下C²+B² =2|AD|
證法6:圓
作Rt△ABC外接圓
∵∠BAC=90°
∴AB是直徑(90°的圓周角所對的弦是直徑)
∴D是圓心,AD是半徑
∴AB=2AD
證法7:餘弦定理
設三角形的兩條直角邊為a、b,斜邊為c,中線為d。
∵a²+b²=c²,且d為斜邊的中線,
∴對同一個角B,可得:
cosB=(a²+c²-b²)/2ac=(a²+1/4c²-d²)/ac
化簡後為:a²-1/2c²+b²=2d²
∵a²+b²=c²,∴代入后可得:1/2c²=2d²,
d1=1/2c,d2=-1/2c(不合題意,捨去)
∴d=1/2c,命題得證。
證法8:反證法
假設 BD != AD
1) CD > AD =>∠CAD >∠DCA (三角形大邊對大角)
BD > AD =>∠BAD >∠ABD
=>∠CAD+∠BAD >∠ABD+∠ACD
=>∠ABD+∠ACD <90°
=>CD > AD 不成立
2)同理可得 CD
=> CD =AD
如果一個三角形一邊上的中線等於這邊的一半,那麼這個三角形是直角三角形,且該邊是斜邊。
幾何語言:在△ABC中,AD是中線,且BC=2AD,則∠BAC=90°。
延長AD到E,使DE=AD,連接BE,CE
∵BD=CD,AE=2AD=BC
∴四邊形ABEC是矩形(∵對角線互相平分且相等)
∴∠BAC=90°
∵AD=BD=CD
∴A,B,C在以D為圓心,BD為半徑的圓上
那麼BC是直徑,根據圓周角定理的推論,直徑所對的圓周角是直角。
∴∠BAC=90°
過D作DE⊥AB,垂足為E。
∵AD=BC/2=BD
∴E是AB中點(三線合一)
∴DE∥AC(三角形中位線定理)
∴AC⊥AB,即∠BAC=90°
向量證明
設向量AD= d,向量AB= c,向量AC= b,向量BC= a
∵AD是中線
∴ b+ c=2 d
兩邊平方,去括弧得
| b|²+2 b· c+| c|²=4| d|²
又∵| a|=2| d|
∴| a|²=4| d|²=| b|²+2 b· c+| c|²~~~①
而 a= b- c
兩邊平方,去括弧得
| a|²=| b|²-2 b· c+| c|²~~~②
聯立①和②解得 b· c=0
∴ b⊥ c,即∠BAC=90°
解析幾何證明
以D為原點,BC所在直線為x軸建立直角坐標系。設B(-d,0),C(d,0),A(a,b),其中d>0且b≠0
∵|AD|=|CD|
∴d= 根號下A²+B²,即 D²=A²+B²
KAB=b/(a+d),KAC =b/(a-d)
KAB*KAC=b²/(a²-d²)=b²/(-b²)=-1
∴AB⊥AC,即∠BAC=90°
注意a≠d,若a=d則表示A和C的橫坐標相同,即AC⊥x軸,這樣就有了Rt∠ACB。而直角邊BC邊上的中線AD是不可能等於直角邊BC的一半的。∴a≠d,AC斜率存在。
如果直角三角形斜邊上一點與直角頂點的連線與該點分斜邊所得兩條線段中任意一條相等,那麼該點為斜邊中點。
幾何語言:在Rt△ABC中,∠ACB=90°,D在AB上,且AD=CD(或BD=CD),則AD=BD。
下面只證明當AD=CD時的情況,BD=CD只需要改字母即可。
在Rt△ABC中,∠ACB=90°
∵AD=CD
∴∠A=∠ACD(等邊對等角)
∵∠A+∠B=90°(直角三角形兩銳角互余),∠ACD+∠BCD=∠ACB=90°
∴∠B=∠BCD(等角的餘角相等)
∴BD=CD(等角對等邊)
∴AD=BD(等量代換)
作DE⊥AC,垂足為E
∵AD=CD
∴E是AC中點(三線合一)
∵BC⊥AC
∴DE∥BC
∴D是AB中點(三角形中位線定理逆定理,或平行線等分線段定理的推論)
延長CD到E,使DE=CD,連接AE
則AD=CD=CE/2
由逆定理1可知∠CAE=90°
∵∠ACB=90°
∴AE∥BC
∴∠AED=∠BCD
∵∠ADE=∠BDC,DE=CD
∴△ADE≌△BDC(ASA)
∴AD=BD
解析幾何證明:
以C為原點,CB、CA為坐標軸建系,設B(b,0)、A(0,a)
又設AD/DB=t,t>0,由定比分點坐標公式得
D(TB/1+T * A/1+T)
∵|CD|=|AD|
由兩點間距離公式,有根號下(TB/1+T)²+(A/1+T)²=根號下(TB/1+T)²+[(A/1+t)-A}²
整理得A²/(1+t)²=a²t²/(1+t)²
∴1=t²,t=1
即AD=DB
餘弦定理證明:
設兩個銳角A,B所對的直角邊為a,b,斜邊為c,AD=CD=d。
∴對同一個角A,有:
cosA=(c²+b²-a²)/2bc=(1/4c²+b²-d²)/bc
∴(c²+b²-a²)=2×(1/4c²+b²-d²)
化簡后得:1/2c²=b²+a²-2d²。
∵a²+b²=c²,∴1/2c²=2d²,d=1/2c(d=-1/2c捨去,不合題意)
∴AD=CD=1/2c,BD=AC-AD=c-1/2c=1/2c=AD=CD。
證法6
設 三角形的兩個直角邊長度分別為 a ,b,將三角形ABC 頂點A放置,AC在+Y 軸線 AB在+x軸
直角邊AC對應的複數為 ai 直角邊 BC對應的複數為b
斜邊BC 對應的複數為z1=-b+ai, BC中點D ,BD的複數為做z2=1/2 *z1=-b/2+ai/2
AD 對應的複數為 z2-A =-b/2+ai/2-ai=-b/2-ai/2 顯然 |z2-A| =|z1|/2 所以中線等於斜邊的一半
目錄