模糊數

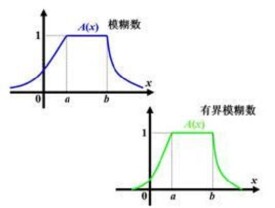
當滿足以下條件的模糊集合A，即可被稱為模糊數Ã：

A 必須是一個正規 (Normal) 模糊集合。

αA對所有的 必須是一個封閉區間 (也就是必須是凸集合)。

0+A (A的底集) 必須是有界的。

"模糊數"在工具書中的解釋

利用凸模糊集可以定義模糊數。模糊數的討論是在區間數的基礎上，所謂區間數就是把一個閉區間[a,b]作為一個數來處理，從而形成計算數學的一個新的分支——區間分析。

在YagerandFilev所提出的模糊數權重思想之上，針對模糊數的排序，提出了一種新的排序的方法，這種方法的提出很好的解決了以前存在的問題。在論文中，分析了公式要處理的六種情況，並且，推導出了運用公式處理這六種情況所產生的結果，這樣以來，就可以在處理排序問題的時候直接運用公式推導出的結果進行討論，簡化了以往討論的複雜性。進一步用圖象來分析公式的幾何意義，運用matlab給出了形變因子對模糊數的影響的圖像，經過圖像分析之後，我們在形變因子對隸屬度函數影響的方面有個很清晰的認識。最後針對滿意度公式，提出具有代表性的數值例子進行說明。

在不同的形變因子影響之下，得到排序的結果也不相同。公式的提出很好的處理了結果的單一性，可以根據對結果所產生的圖像進行分析，得出需要的結果。