計算數學
由數學等學科交叉滲透的專業
計算數學是由數學、物理學、計算機科學、運籌學與控制科學等學科交叉滲透而形成的一個理科專業。
計算數學也叫做數值計算方法或數值分析。主要內容包括代數方程、線性代數方程 組、微分方程的數值解法,函數的數值逼近問題,矩陣特徵值的求法,最優化計算問題,概率統計計算問題等等,還包括解的存在性、唯一性、收斂性和誤差分析等理論問題。
五次及五次以上的代數方程不存在求根公式,因此,要求出五次以上的高次代數方程的解,一般只能求它的近似解,求近似解的方法就是數值分析的方法。對於一般的超越方程,如對數方程、三角方程等等也只能採用數值分析的辦法。怎樣找出比較簡潔、誤差比較小、花費時間比較少的計算方法是數值分析的主要課題。
在求解方程的辦法中,常用的辦法之一是迭代法,也叫做逐次逼近法。迭代法的計算是比較簡單的,是比較容易進行的。迭代法還可以用來求解線性方程組的解。求方程組的近似解也要選擇適當的迭代公式,使得收斂速度快,近似誤差小。
在線性代數方程組的解法中,常用的有塞德爾迭代法、共軛斜量法、超鬆弛迭代法等等。此外,一些比較古老的普通消去法,如高斯法、追趕法等等,在利用計算機的條件下也可以得到廣泛的應用。
在計算方法中,數值逼近也是常用的基本方法。數值逼近也叫近似代替,就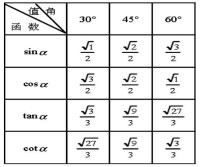 是用簡單的函數去代替比較複雜的函數,或者代替不能用解析表達式表示的函數。數值逼近的基本方法是插值法。初等數學里的三角函數表,對數表中的修正值,就是根據插值法製成的。
是用簡單的函數去代替比較複雜的函數,或者代替不能用解析表達式表示的函數。數值逼近的基本方法是插值法。初等數學里的三角函數表,對數表中的修正值,就是根據插值法製成的。

三角函數
在遇到求微分和積分的時候,如何利用簡單的函數去近似代替所給的函數,以便容易求到和求積分,也是計算方法的一個主要內容。微分方程的數值解法也是近似解法。常微分方程的數值解法由歐拉法、預測校正法等。偏微分方程的初值問題或邊值問題,
藉助於某量已知的個別值或與其有關的其他量來逼近或精確地尋求該量的一種方法。以插值為基礎的解數學問題的一個完整的近似方法系列已經發展起來了。
計算數學中最重要的是對於函數的插值(Interpolation)的構造方法的問題泛函和運算元的插值在構造計算方法中也已得到廣泛的應用。函數的近似表示和計算,函數的插值視為逼近該函數的方法之一。
有限元素法是近代才發展起來的,它是以變分原理和剖分差值作為基礎的方法。在解決橢圓形方程邊值問題上得到了廣泛的應用。有許多人正在研究用有限元素法來解雙曲形和拋物形的方程。
計算數學的內容十分豐富,它在科學技術中正發揮著越來越大的作用。
計算問題可以說是現代社會各個領域普遍存在的共同問題,工業、農業、交通運輸、醫療衛生、文化教育等等,哪一行哪一業都有許多數據需要計算,通過數據分析,以便掌握事物發展的規律。研究計算問題的解決方法和有關數學理論問題的一門學科就叫做計算數學。計算數學屬於應用數學的範疇,它主要研究有關的數學和邏輯問題怎樣由計算機加以有效解決。
模糊數學是一門新興學科,它已初步應用於模糊控制、模糊識別、模糊聚類分析、模糊決策、模糊評判、系統理論、信息檢索、醫學、生物學等各個方面。在氣象、結構力學、控制、心理學等方面已有具體的研究成果。然而模糊數學最重要的應用領域是計算機職能,不少人認為它與新一代計算機的研製有密切的聯繫。模糊數學是以不確定性的事物為其研究對象的。在模糊數學中,已有模糊拓撲學、模糊群論、模糊圖論、模糊概率、模糊語言學、模糊邏輯學等分支。
算術、初等代數、高等代數、數論、歐式幾何、非歐幾何、解析幾何、微分幾何、代數幾何學、射影幾何學、拓撲學、分形幾何、微積分學、實變函數論、概率和數理統計、複變函數論、泛函分析、偏微分方程、常微分方程、數理邏輯、模糊數學、運籌學、突變理論、數學物理學。
計算數學也叫做數值計算方法或數值分析。
應用數學是應用目的明確的數學理論和方法的總稱,研究如何應用數學知識到其它範疇(尤其是科學)的數學分枝,可以說是純數學的相反。包括微分方程、向量分析、矩陣、傅里葉變換、復變分析、數值方法、概率論、數理統計、運籌學、控制理論、組合數學、資訊理論等許多數學分支,也包括從各種應用領域中提出的數學問題的研究。計算數學有時也可視為應用數學的一部分。
圖論應用在網路分析,數論應用在密碼學,博弈論、概率論、統計學、應用在經濟學,都可見數學在不同範疇的應用。
計算數學是研究如何用計算機解決各種數學問題的科學,它的核心是提出和研究求解各種數學問題的高效而穩定的演演算法。高效的計算方法與高速的計算機是同等重要的,計算作為認識世界改造世界的一種重要手段,已與理論分析、科學實驗共同成為當代科學研究的三大支柱。計算數學主要研究與各類科學計算與工程計算相關的計算方法,對各種演演算法及其應用進行理論和數值分析,設計與研究用數值模擬方法代替某些耗資巨大甚至是難於實現的實驗,研究專用或通用科學工程應用軟體和數值軟體等。近年來,計算數學與其他領域交叉滲透,形成了諸如計算力學,計算物理,計算化學,計算生物等一批交叉科學,在自然科學、社會科學、工程技術及其國民經濟的各個領域得到了日益廣泛的應用。
培養方向
1、微分方程數值解法及其應用
2、優化與控制理論及其數值計算
3、數值代數與數值軟體
擁有數學國家一級重點學科的高校:
| 北京大學 |
| 清華大學,北京協和醫學院—清華大學醫學部 |
| 北京師範大學 |
| 南開大學 |
| 吉林大學 |
| 復旦大學 |
| 南京大學 |
| 浙江大學 |
| 中國科學技術大學 |
| 山東大學 |
| 四川大學 |
僅擁有計算數學國家二級重點學科的高校(不含已擁有數學國家一級重點學科的高校):
《計算數學》於1964年創刊,1979年復刊,首任主編是在國際上享有盛譽的已故著名科學家,獨立於西方創立有限元方法的中國科學院院士馮康教授(馮康院士的哈密爾頓系統的辛幾何演演算法獲國家自然科學獎一等獎)。 《計算數學》編委會由國內著名計算數學和應用數學專家組成,編委會成員均是各個學科的帶頭人,其中有三位是中國科學院院士,一位是中國工程院院士。
《計算數學》是數值計算的理論、分析及其應用的學術性刊物,是中國在計算數學領域公開發行的學術水平最高的期刊,在國內外享有很高的知名度。它主要刊登國內外專家、學者、科研人員具有新思想、新觀點、創造性強的最新研究成果的論文、各種新的計算方法的理論分析以及在科學與工程等學科中的實際應用。同時也討論國際上的熱點問題,內容涉及計算數學以及與計算數學相關的工程的各個方面。
期刊名稱:計算數學
主辦單位:中國科學院數學與系統科學研究院
出版周期:季刊
出 版 地:北京市
語言種類:中文
開本尺寸:16開
國際刊號:0254-7791
國內刊號:11-2125/O1
郵發代號:2-521
創刊時間:1979年
該刊被以下資料庫收錄:
SA 科學文摘(英)(2011)
CBST 科學技術文獻速報(日)(2009)
中國科學引文資料庫(CSCD—2008)
中文核心期刊(2008)
中文核心期刊(2004)
中文核心期刊(2000)
中文核心期刊(1996)
中文核心期刊(1992)
20世紀以來,因為計算機的廣泛應用,計算數學得到了長足發展,而計算數學理論的發展又促進了計算機和信息科學的進步。雖然在國內計算數學還沒有得到足夠的重視,但在國外計算數學是最熱門的學科之一。計算數學的主要研究方向包括數值泛函分析與連續計算複雜性理論、數值偏微與有限元、非線性數值代數及復動力系統、非線性方程組的數值解法、數值逼近論、計算機模擬與信息處理等、工程問題數學建模與計算。發展最好的方向已經與應用數學的CAGD方向合二為一,因為二者的核心都是數值計算,並以計算機編程為手段。

計算數學
蔡小昊(2006級計算數學碩士研究生):計算數學在國內和國際上都是一個很重要的學科,它主要對科學工程計算等問題進行研究。因為學科交叉會帶來很多新生的研究方向,所以計算數學的研究方向非常多。最熱的方嚮應該是微分方程的數值求解、數值代數和流形學習,特別是流形學習已經熱了幾年,估計還會繼續熱下去。
潘一力(2007級計算數學碩士研究生):作為交叉型學科,發展前景廣闊。很多有實際物理應用背景的研究(如流體力學、光波導、光子晶體等)以及很多需要解決的問題,工科的人往往因缺乏實際的數學計算能力對數學問題無從下手,不知如何解決,這正需要數學系的學生利用自身的數學背景著手去解決這些問題。
Sophia(2006級計算數學碩士研究生):簡言之,計算數學就是為物理學和工程學作計算的一門專業。我個人覺得有限元是今後的熱門方向。
