差分方程
自動控制與設計、數值計算等
在數學上,遞推關係(recurrence relation),也就是差分方程(difference equation),是一種遞推地定義一個序列的方程式:序列的每一項目是定義為前一項的函數。某些簡單定義的遞推關係式可能會表現出非常複雜的(混沌的)性質,他們屬於數學中的非線性分析領域。
所謂解一個遞推關係式,也就是求其解析解,即關於n的非遞歸函數。
差分方程是微分方程的離散化。一個微分方程不一定可以解出精確的解,把它變成差分方程,就可以求出近似的解來。
比如 dy+y*dx=0,y(0)=1 是一個微分方程, x取值[0,1]
(註:解為y(x)=e^(-x));
要實現微分方程的離散化,可以把x的區間分割為許多小區間 [0,1/n],[1/n,2/n],...[(n-1)/n,1]
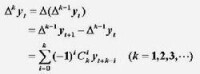
差分方程
利用y(0)=1的條件,以及上面的差分方程,就可以計算出 y(k/n) 的近似值了。
§1 基本理論1. 差分
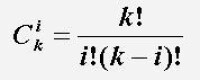
差分方程
Δxn=xn+1-xn
對新數列再應用差分運算元,有
Δ2xn=Δ(Δkxn).
性質1 Δk(xn+yn)=Δkxn+Δkyn
性質2 Δk(cxn)=cΔkxn
性質3 Δkxn=∑(-1)jCjkXn+k-j
性質4 數列的通項為n的無限次可導函數,對任意k>=1,存在η,有 Δkxn=f(k)(η)
差分方程
定義8.1 方程關於數列的k階差分方程:
xn-a1xn-1-a2xn-2-……akxn-k=b (n=k,k+1,……)
其中a1,a2,------ak 為常數, ak≠0. 若b=0,則該方程是齊次方程
關於λ 的代數方程
λk-a1λk-1-------ak-1λ-ak=0
為對應的特徵方程,根為特徵值。
1. 實驗內容與練習
2.1 差分
例1 Xn={n3},求各階差分數列:
xn △xn △2xn △3xn △4xn
1 7 12 6 0
8 19 18 6 0
27 37 24 6 0
64 61 30 6
125 91 36
216 127
343
可見,{n3},三階差分數列為常數數列,四階為0。
練習1 對{1},{n},{n2},{n4},{n5},分別求各階差分數列。
練習2 {C0n-1}{C1n-1}{C2n-1},{C4n-1},分別求各階差分數列.
{Xn}的通項為n的三次函數,
Xn=a3n3+a2n2+a1n+a0
證明它為常數數列。
證明 由Xn=a3n3+a2n2+a1n+a0可直接計算。
定理8,1 若數列的通項是關於n 的k次多項式,則 k 階差分數列為非零數列,k+1階差分數列為0。
練習3 證明定理8.1。
定理8.2 若{Xn}的 k 階插分為非零常數列,則{Xn}是 n的 k次多項式,
練習4 根據差分的性質證明定理8。2
例2。求∑i3
例4
解 設Sn=∑i3 表
Sn △Sn △2Sn △3Sn △4Sn △5Sn
18191860
927372460
3664613060
100125913660
22521612742
441343169
784512
1296
設Sn=a4n4+a3n3+a2n2+a1n+a0,s1=1,s2=9,s3=36,s4=100,s5=225,得
a0=0,a1=0,a2=1/4,a3=1/2,a4=1/4.
所以, Sn=(1/4)n4+(1/2)n3+(1/4)n2.
練習 {Xn}的通項Xn為n的k次多項式,證明∑xi為n的 k+1次多項式;求 ∑i4.
由練習 2 {Crn-1}可得。
2.2差分方程
對於一個差分方程,如果能找出這樣的數列通項,將它帶入差分方程后,該方程成為恆等式,這個通項叫做差分方程的解。
例3 對差分方程 xn-5xn-1+6xn-2=0,可直接驗證xn=c13n+c22n是該方程的解。
例3中的解中含有任意常數,且任意常數的個數與差分方程的階數相同。這樣的解叫做差分方程的通解。
若k階差分方程給定了數列前k項的取值,則可以確定通解的任意常數,得到差分
的特解。
例4對差分方程xn-5xn-1+6xn-2=0,若已知x1=1,x2=5,則可以得到該差分方程的特解為xn=3n-2n.
我們首先研究齊次線性差分方程的求解。
xn=rxn-1
對一階差分方程
x1=a
顯然有xn=arn-1。因此,若數列滿足一階差分方程,則該數列為一個等比數列。
例5 求Fibonacci數列{Fn}的通項,其中F1=1,F2=1,Fn=Fn-1+Fn-2.
Fibonacci數列的前幾項為:1,1,2,3,5,8,13,21,34,55,89,…。該數列有著非常廣泛的應用。
Fibonacci數列所滿足的差分方程為 Fn-Fn-1-Fn-2=0,
其特徵方程為 λ2-λ-1=0
其根為λ1=,λ2= .利用λ1λ2可將差分方程寫為
Fn-(λ1+λ2)Fn-1+λ1λ2Fn-2=0,
即Fn-λ1Fn-1=λ2(Fn-1-λ1Fn-2)
數列{Fn-λ1Fn-1}滿足一個一階差分方程.顯然 ( )
同理可得 ( )
由以上兩式可解出 的通項。
練習9 證明若數列{ }滿足二階差分方程,其特徵方程由兩個不相等的根,則 為該差分方程的兩個特解。從而其通解為。
由練習9,若二階差分方程的特徵方程有兩個不相等的根,可寫出其通解的一般性式。再由 的值可解出其中的係數,從而寫出差分方程的特解。
練習10 具體求出 Fibonacci數列的通項,並證明。那麼,若二階線性齊次差分方程有兩個相等的根,其解有如何來求呢?
設二階線性齊次差分方程的特徵方程有兩個相等的根,則差分方程可寫為。差分方程的兩邊同時除以,有。設,則 (n>=3)。由於該式在 n>=3式均成立,我們將它改寫為 (n>=1)。(8.2)
方程(8.2)的左邊是 的二階差分,從而有,於是 是n的一次函數,設為 則有。上是即為差分方程的通解。
練習11 證明:若數列{ } 所滿足的三階差分方程的特徵方程由三個相等的根,則差分方程的通解為。
一般的,設 ···,為差分方程的特徵方程所有不同的解,其重數分別為 ···, ,則差分方程對應於其中的根(i=1,2,···,l)的特解 ···。
對於一般的k階齊次線性差分方程,我們可以通過其特徵方程得到上述形式的k個特解,進而得到差分方程的通解。
練習12 若數列{ } 滿足差分方程
且 求{ }的通項。
例6 若實係數差分方程的根為虛數,則其解也是用虛數表示的,這給討論問題帶來不便。差分方程
xn-2xn-1+4xn-2=0
的特徵值為 i.若x1=1,x2=3,由下面的程序易求出其特解為:
xn=( )(1+ i)n+(- )(1- i)n
Clear[x1,x2,c1,c2,l1,l2,solution];
x1=1;x2=3;
solution=Solve[1^2-2l+4==0,1];
l1=l/.solution[[1,1]];
l2=l/.solution[[2,1]];
c=Solve[ {c1*l1+c2*l2==x1,c1*l1^2+c2*l2^2==x2},{c1,c2}];
c1=Simplify[ Re[c1]]+Simplify]*I;
c2=Simplify[Re[c2]]+Simplify]*I;
Print[“xn=(“,c1,”)(“,l1,”)^n+(“,c2,”)(“,l2,”)^n”]
解的形式相當複雜,是否可以將它們用實數表示呢?
設 =rei,則 =re,我們可將(8.4)中的表達式改寫為
xn=re (2e )n+re (2e )\n
=r
=2r Cos( )
=(2rCos )
=
可以看出,通項可以寫成 的形式.那麼,與 是不是差分方程的特解呢?
練習13 驗證 與 是差分方程(8.3)的特解.
對於差分方程(8.3),我們找出了它的兩個實型的特解,從而可以將通解表示成實數的形式。這一方法對於一般的方程也是成立的.
練習14 設 的兩個特徵值為 .證明該差分方程的通解可表示為 .
練習 15 用實數表示差分方程 的特解.
上次我們討論了其次線性差分方程的求解方法。那麼,非齊次線性差分方程是否可以化為齊次線性差分方程呢䲁
練習16 若已知非齊次線性差分方程
··· (8.5)
的一個特解為 求證:若令 則 滿足齊次差分方程
···
由練習16,若已知非齊次線性差分方程(8.5)的一個特解,就可以將它化為齊次線性差分方程.
顯然方程(8.5)的最簡單的形式為(其中p為常數),代入(8.5)得
···
若 ··· 則有
稱p = 為非齊次線性差分方程(8.5)的平衡值。在(8.5)中,令 則有
由,得
.
從而可將原來的非齊次線性差分方程化為齊次線性差分方程.
如果方程(8.5)的平衡值不存在,可以將方程(8.5)中所有的n換為n+1,得到
(8.6)
方程(8.6)和(8.5)相減得
.
於是可將原來的非齊次線性差分方程化為高一階的齊次線性差分方程.
練習17 分別求差分方程 及 的通解.
2.3代數方程求根
由 Fibonacci數列的性質,我們可以用 來逼近,用這一性質可以來計算 的近似值。一般地,對a>0,可以用構造差分方程的方法來求 的近似值.
對給定的正數a,設λ1= ,λ2= ,則λ1 ,λ2是方程λ2-2λ+(1+a)=0的根。該方程是差分方程 的特徵方程。於是,選定,利用差分方程 可以構造一個數列{ }.
練習 18 證明:若a>1,對任意的 >0,>0,若 ≠ ,則按上述法構造的數列{ }滿足
.這樣,我們得到了計算 的一個方法:
1. 給定(作為誤差控制),任取初始值,令n=1;
2. 若
則終止計算,輸出結果;否則,令n :=n+1,轉第3步;
3. 令,轉第2步.
練習 19 對a=1.5,10,12345,用上述方法求 .
上述方法的收斂速度不夠快,我們可以加以改進
設整數u滿足,令,則,是方程 的兩個根.
練習 20 根據上面的差分方程的構件數列{ x },使得
.
練習 21 對練習19中的a,用上面的方法來計算,並比較兩種方法的收斂速度.
代數方程
(8.7)
是差分方程(8.1)的特徵方程,是否可以用此差分方程來求解方程(8.7)呢?
設徠方程(8.7)有k個互不相同的根滿足
, (8.8)
則對應的差分方程的通解形式為
.
練習 22 設方程(8.7)的根滿足條件(8.8),任取初始值 用差分方程(8.1)(取b=0)構造數列{ }.若通解中 的係數 ≠0,證明:
.
利用練習22得到的結論,我們可以求多項式方程的絕對值最大的根.
練習 23 求方程 的絕對值最大的根.
事實上,若方程(8.7)的互不相同的根滿足
≥ ≥…≥
(其重數分別為),則練習22中的結論仍然成立.
2.4 國民收入4 國民收入的穩定問題
一個國家的國民收入可用於消費,再生產的投資等。一般地說,消費與再生產投資都不應該沒有限制。合理的控制各部分投資,能夠使國民經濟處於一種良性循環之中。如何配各部分投資的比例,才能使國民經濟處於穩定狀態呢?這就是本節要討論的問題。
我們首先給出一些假設條件:
1. 國民收入用於消費、再生產投資和公共設施建設三部分。
2. 記 分別為第k個周期的國民收入水平和消費水平。的值與前一個周期的國民收入成正比例。即 =A,(8.9)其中A為常數(03. 用 表示第k個周期內用於再生產的投資水平,它取決於消費水平的變化,即 . (8.10)
4. G表示政府用於公共設施的開支,設G為常數。由假設1有 . (8.11)上式是一個差分方程,當給定 的值后,可直接計算出國民收入水平(k=2,3,…)來觀察其是否穩定。
例7 若,計算可得表8.3中數據。
表8.3 Y 的值的變化
k 2 3 4 5 6 7 8 9 10 11
11.0 24.5 35.8 39.1 32.9 20.3 7.48 0.95 3.93 15.0
k 12 13 14 15 16 17 18 19 20 21
28.5 37.8 38.2 29.5 16.0 4.58 0.82 6.65 19.2 32.1
我們可以畫出 的散點圖來觀察其變化。其計算及畫圖的程序如下:
y0=2;y1=2;a=0.5;b=2;g=10;
y={y0,y1};
For[k=1,k<=20,k++,
Y2=a(1+b)*y1-b*a*y0+g;
Y=Append[y,y2];
Y0=y1,y1=y2]
YListPlot[y,PlotJoined True,
PlotStyle Thickness[0.012]]
圖8.1 國民收入 的變化
由圖8.1利用發現,又例7的數據得出的 的呈現出周期變化的跡象。
練習 24設,對於表8.4中的參數A,B,分別計算(k=2,3,…)並畫圖觀察 的變化。
表8.4 參數A,B的取值
A 1/2 1/2 1/2 8/9 9/10 3/4 4/5
B 1 2 3 1/2 1/2 3 3
可以看出,隨著參數的值不同,國民收入水平(k=2,3,…)的穩定性呈現出不同的狀態。
那麼,參數滿足什麼條件時,國民收入水平才處於穩定發展之中呢?
差分方程(8.11)是一個常係數非齊次線性差分方程。由A<1容易求出其平衡值為
令 可得
.
其特徵值為
若 則
其中 為 的幅角。
從而可的差分方程的解為
其中 為常數。
若 易見{ }為一周期函數在 ---的取值,從而{ }呈周期變化的狀態。正如在例7中所見到的。
練習25 若 在 及 的情形下,討論{ }的變化趨勢。國民收入會穩定發展嗎?
練習26 若,國民收入在什麼條件下會穩定發展?
本實驗涉及的Mathematica軟體語句說明
1. solution=Solve[1^2-2l+4==0,1];
l1=1/.solution[[1,1]];
l2=l/.solution[[2,1]];
將方程l^2-2l+4==0的兩根分別賦值給l1及l2.
2. c=Solve[{c1*l1+c2*l2==x1,c1*l1^2+c2*l2^2==x2},{c1,c2}];
{c1,c2}={c1,c2}/.c[];
將方程組{c1*l1+c2*l2==x1,c1*l1^2+c2*l2^2==x2}的解賦值給c1及c2.
3. c1=Simplify[Re[c1]]+Simplify]*I
將複數c1化簡.
一、差分的概念
設函數yt=f(t)在t=…,-2,-1,0,1,2,…處有定義,對應的函數值為…,y-2,y-1,y0,y1,y2,…,則函數yt=f(t)在時間t的一階差分定義為 Dyt=yt+1-yt=f(t+1)-f(t)。
依此定義類推,有 Dyt+1=yt+2-yt+1=f(t+2)-f(t+1),Dyt+2=yt+3-yt+2=f(t+3)-f(t+2),………………
一階差分的性質
(1) 若yt=C(C為常數),則Dyt=0;
(2) 對於任意常數k,D(KYT)=kDyt;
(3) D(yt+zt)=Dyt+Dzt。
函數yt=f(t)在時刻t的二階差分定義為一階差分的差分,即
D2yt= D (D yt)= D yt+1- D yt
=(yt+2-yt+1)-(yt+1-yt)=yt+2-2yt+1+yt.
依此定義類推,有
D2yt+1= Dyt+2- Dyt+1=yt+3-2yt+2+yt+1,D2yt+2= Dyt+3- Dyt+2=yt+4-2yt+3+yt+2,………………
類推,計算兩個相繼的二階差分之差,便得到三階差分
D3yt= D2yt+1- D2yt=yt+3-3yt+2+3yt+1-yt,
D3yt+1= D2yt+2- D2yt+1=yt+4-3yt+3+3yt+2-yt+1, ………………
一般地,k階差分(k為正整數)定義為
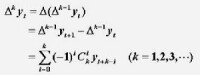
差分方程
設{ut,t=0,±1…}為實序列,若滿足如下關係式ut-ᵠ1ut-1-…-ᵠput-p=h(t),其中ᵠ1,ᵠ2…,ᵠp為實數,h(t)為t的已知實函數,則稱上式為{ut}所滿足的線性差分方程。
如將上式中的確定性函數ut,h (t)代之以統計特性已知的隨機序列,於是便得到線性隨機差分方程。在時間序列分析中並不討論這樣廣泛的模型,只涉及一種特殊的線性隨機差分方程:
xt-ᵠ1xt-1-…-ᵠpxt-p=εt-θ1εt-1-…-θqεt-g
其中ᵠ1, …,ᵠp,及θ1, …,θg為實數, {xt}是零均值平穩序列,{εt}是平穩白雜訊序列,且當s>t時Eεsxt=0上述特定的線性隨機差分方程就是時間序列分析中的ARMA (p,g) 模型。
形如yt+n+a1(t)yt+n-1+a2(t)yt+n-2+…+an-1(t)yt+1+an(t)yt=f(t)的差分方程,稱為n階非齊次線性差分方程。其中a1(t),a2(t),…,an-1(t),an(t)和f(t)都是t的已知函數,且an(t)≠0,f(t)≠0。
而形如yt+n+a1(t)yt+n-1+…+an-1(t)yt+1+an(t)yt=0的差分方程,稱為n階齊次線性差分方程。其中ai(t)(i=1,2,…,n)為t的已知函數,且an(t)≠0。
如果ai(t)=ai(i=1,2,…,n)均為常數(an≠0),則有
yt+n+a1yt+n-1+a2yt+n-2+…+an-1yt+1+anyt=f(t),
yt+n+a1yt+n-1+a2yt+n-2+…+an-1yt+1+anyt=0。
分別稱為n階常係數非齊次線性差分方程和n階常係數齊次線性差分方程。
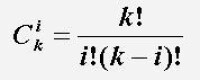
差分方程
含有未知函數yt=f(t)以及yt的差分Dyt, D2yt,…的函數方程,稱為(簡稱);出現在差分方程中的差分的最高階數,稱為。n階差分方程的一般形式為
F(t,yt,Dyt,…, Dnyt)=0,
其中F是t,yt, Dyt,…, Dnyt的已知函數,且Dnyt一定要在方程中出現。
含有兩個或兩個以上函數值yt,yt+1,…的函數方程,稱為,出現在差分方程中未知函數下標的最大差,稱為。n階差分方程的一般形式為
F(t,yt,yt+1,…,yt+n)=0,
其中F為t,yt,yt+1,…,yt+n的已知函數,且yt和yt+n一定要在差分方程中出現。
三、差分方程的解
如果將已知函數yt=j(t)代入方程F(t,yt,yt+1,…,yt+n)=0,使其對t=…,-2,-1,0,1,2,…成為恆等式,則稱yt=j(t)為方程的解。含有n個任意(獨立)常數C1,C2,…,Cn的解
yt=(t,C1,C2,…,Cn)
稱為。在通解中給任意常數C1,C2,…,Cn以確定的值所得的解,稱為。
一、存款模型
設St為t期存款總額,i為存款利率,則St與i有如下關係式:
St+1=St+iSt=(1+i)Si, t=0,1,2,…,
其中S0為初始存款總額。
二、動態供需均衡模型(蛛網定理)
設Dt表示t期的需求量,St表示t期的供給量,Pt表示商品t期價格,則傳統的動態供需均衡模型為:
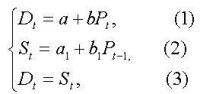
差分方程
(1)式表示t期(現期)需求依賴於同期價格;
(2)式表示t期(現期)供給依賴於(t-1)期(前期)價格。
(3)式為供需均衡條件。
若在供需平衡的條件下,而且價格保持不變,即 Pt=Pt-1=Pe,靜態均衡價格
需求曲線與供給曲線的交點(Pe ,Qe)即為該種商品的靜態均衡點。
動態供需均衡模型的等價差分方程
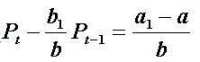
差分方程
方程的通解為
若初始價格P0已知時,將其代入通解,可求得任意常數A=P0-Pe ,此時,通解改寫為
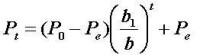
差分方程
差分方程
動態價格Pt隨著t的無限增大逐漸地振蕩趨近於靜態均衡價格Pe 。
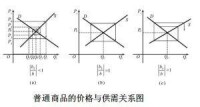
差分方程
設Yt表示t期國民收入,Ct為t期消費,It為t期投資,DI0為自發(固定)投資,I為周期固定投資增量。凱恩斯國民經濟收支動態均衡模型為:
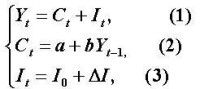
差分方程
在(1)(2)(3)式中消去Ct和It,得到一階常係數非齊次線性差分方程:
Yt-bYt-1=a+I0+DI 方程的一個特解
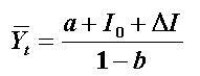
差分方程
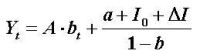
差分方程
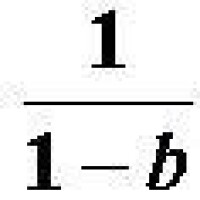
差分方程
四、哈羅德(Harrod.R.H)經濟增長模型
設St為t期儲蓄,Yt為t期國民收入,It為t期投資,s稱為邊際儲蓄傾向(即平均儲蓄傾向),0<s<1,k為加速係數。哈羅德宏觀經濟增長模型為:
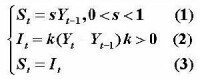
差分方程
(1)式表示t期儲蓄依賴於前期的國民收入;(2)式表示t期投資為前兩期國民收入差的加速,且預期資本加速係數k為常數;(3)式為均衡條件。
經整理后得齊次差分方程
其通解為
其中A為任意常數,
,哈羅德稱之為“保證增長率”其經濟意義就是:如果國民收入Yt按保證增長率
增長,那麼就能保證t期儲蓄與t期投資達到動態均衡,即It=St , t=0,1,2,…。
五、薩繆爾森(Samuelson P.A)乘數加速數模型
設Yt為t期國民收入,Ct為t期消費,It為t期投資,G為政府支出(各期均相同)。薩繆爾森將乘數和加速數兩個參數同時引進而得到國民經濟收支均衡模型(也稱為乘數-加速數模型):
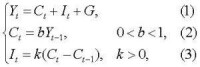
差分方程
將(2)(3)兩式代入(1)並經整理后得:Yt-b(1+k)Yt-1+bkYt-2=G.其特解
其經濟意義為:國民收入的均衡值等於凱恩斯乘數
與政府支出自發投資G的乘積。
對應的齊次方程為 Yt-b(1+k)Yt-1+bkYt-2=0,
其特徵方程為 A2-b(1+k)A+bk=0,特徵方程的判別式
差分方程
差分方程
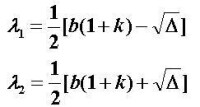
差分方程
差分方程
當
差分方程
。
齊次方程的通解為:
差分方程
當
差分方程
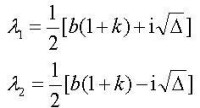
差分方程
差分方程
