法方程

法方程是測量平差計算中的一個重要的方程。它是由平差函數模型線性化后的方程式，以及在V PV=min的條件下所導得的方程式合併而成的聯立方程組。在各種平差函數模型中，方程式的個數總是少於所求未知量的個數，是多解方程，解不惟一，通過法方程則可求得既滿足所有方程式，又滿足V PV=min的一組惟一解。例如，就附有限制條件的條件平差法而言，方程組：

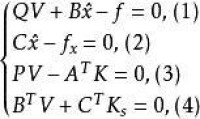
就是它的總法方程，或稱基礎方程。其中(1)，(2)兩式是其函數模型線性化后的方程式，(3)，(4)兩式是在VPV=min”的條件下按條件極值導出的方程式。K和K是求條件極值時分別對應於(1)式和(2)式的拉格朗日乘數向量，在測量中習慣稱為聯繫數向量。若利用(3)式消去V，則得：

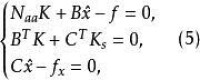
(5)式稱為法方程，其中N=AQA 。其他各種平差方法的總法方程和法方程都可由(1)～(4)式和(5)式簡化而得。

各種平差方法的法方程，其係數陣都是對稱滿秩方陣。但在選取與定位有關的參數進行參數平差時，若網中無起算數據或起算數據不足，誤差方程的係數陣列不滿秩，即產生基準秩虧，則法方程的係數陣將是奇異的。

秩虧網平差亦稱自由網平差。平差計算中的方法之一。它是當測量網選取與定位有關的參數進行參數平差時，其誤差方程式的係數陣為列不滿秩的一種平差方法。引起係數陣列不滿秩的原因有：

1.網中的必要觀測數據不足，使網的形狀無法確定；

2.網中無必要的起算數據，使網的位置、方位和尺度無法確定。

實際工作中，在測量網中總是要進行多餘的觀測，因此通常所稱的“秩虧網”都是指無必要起算數據的測量網。以測量網點坐標為參數的誤差方程為：

由於網中無起算數據，R(B)=t觀測值的個數t，而小於未知參數的個數u，其秩虧數d (=u-t)等於必要起算數據的個數。例如，在水準網中d=1，在平面測邊網、邊角網中d=3，在平面測角網中d=4等。

在VPV=min的條件下可導出求解x^的法方程，由於B列不滿秩，法方程的係數陣將是u階的奇異方陣，其解不惟一。為了獲得一組惟一解，還必須加入新的約束條件，即解向量x^的最小范數條件：

按這些條件求解參數估值的方法分別稱為普通秩虧網平差和加權秩虧網平差。有時還可在部分解向量的范數為最小的條件下計算，如擬穩平差。

擬穩平差是秩虧網平差的方法之一。在無足夠起算數據的測量網中，當選取與定位參數有關的參數進行參數平差時，其誤差方程的係數陣列不滿秩。擬穩平差的做法是：將網中所有待定點分成兩部分，一部分是相對於其他點而言穩定程度較好的點，稱為穩定點；另一部分稱為非穩定點。設非穩定點和穩定點的坐標改正數向量分別為x和x，在進行平差時，為了求得一組惟一解，除了遵循最小二乘準則V PV=min外，還需加入穩定點坐標改正數的范數最小條件x^x^=min，因此，它是在“部分解向量范數最小”條件下的一種求解方法。周江文對擬穩平差進行了深入的研究，在這一研究領域中起到了先導和推動的作用。