費密面
費密面
Fermi surface 描述金屬中電子狀態的動量空間中的等能面。它能量等於電子系統的化學勢,稱費密能量,寫作□□;個面上的能級稱為費密能級。費密分佈函數因為電子遵守。
描述金屬中電子狀態的動量空間中的等能面。它的能量等於電子系統的化學勢,稱費密能量,寫作EF;這個面上的能級稱為費密能級。
因為電子遵守費密-狄喇克統計,所以在絕對零度時,所有能量EEF的電子態都未被佔據。所以費密面也可以看成是絕對零度時這兩種狀態在動量空間的分界面。在溫度T0時,電子佔據的幾率f(E)隨能量E的變化是 其中kB是玻耳茲曼常數。所以在E=EF附近不像在絕對零度時那樣由1陡變到0,而是以EF為中點在一個寬度量級為熱運動能量kBT的範圍內由f(E)≈1變到f(E)≈0(圖1)。電子遵守泡利不相容原理,所以它的躍遷只能從滿態(或部分佔據的狀態)到空態(或沒有完全佔據的狀態)。而物理過程又往往與電子躍遷相關,因此費密面附近的量子態是決定金屬的實際物理性質的最活躍最起作用的量子態。研究一個材料的費密面,對了解這個材料與電子運動有關的各種物理性質是十分重要的。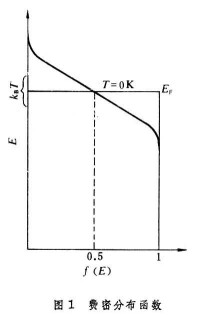 理論計算方法 從理論計算上確定一種材料的費密面的方法如下:首先計算電子的能譜,即各不同波矢k的本徵態的能量E(k),然後把所有的電子按能量E增加的順序,依費密分佈佔據各個狀態,從而確定費密能量EF。如果一個金屬中傳導電子的能譜E(k)可以用自由電子近似描述(例如鹼金屬),則
理論計算方法 從理論計算上確定一種材料的費密面的方法如下:首先計算電子的能譜,即各不同波矢k的本徵態的能量E(k),然後把所有的電子按能量E增加的順序,依費密分佈佔據各個狀態,從而確定費密能量EF。如果一個金屬中傳導電子的能譜E(k)可以用自由電子近似描述(例如鹼金屬),則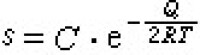 (1)m* 是電子的有效質量。T=0K時
(1)m* 是電子的有效質量。T=0K時 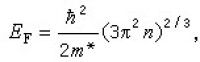 (2)式中 n是電子濃度。在這種情況下費密面就是一個半徑為kF的球,稱為費密球。
(2)式中 n是電子濃度。在這種情況下費密面就是一個半徑為kF的球,稱為費密球。 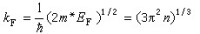 (3)稱為費密波矢,它所對應的電子波包速度
(3)稱為費密波矢,它所對應的電子波包速度 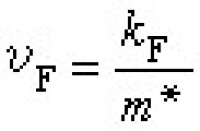 (4)稱為費密速度。實際金屬的電子能譜往往比公式(1)複雜,所以它們的費密面也比球形複雜。在圖2中列舉了兩個例子。
(4)稱為費密速度。實際金屬的電子能譜往往比公式(1)複雜,所以它們的費密面也比球形複雜。在圖2中列舉了兩個例子。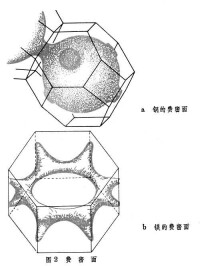 實驗測定方法 利用大型計算機已經可以相當精確地決定實際金屬的費密面。也建立了許多有效的實驗方法。A.P.皮帕德是第一個成功地從實驗上測定金屬的費密面的,他利用了金屬的反常趨膚效應。當金屬受到微波照射時,由於趨膚效應,微波電場只存在於表面附近很薄一層內。如果這塊金屬是純凈的單晶,電子自由程 l大於趨膚層的深度 ξ。費密面上不同速度的電子和微波電場的作用會不同, 當l≥ξ時,這實際上相當於“切”下費密面上速度近似平行於表面的部分。所以,測量各種情況下的表面阻抗,可以獲得費密面的信息。皮帕德就用這辦法得到了銅的費密面。隨後又發展了許多其他方法。常用的方法可以分為兩大類。一大類是與碰撞效應有關的方法。例如探測正電子與金屬中自由電子湮沒時發射的光子的動量分佈的湮沒效應法,測量X 射線被金屬中自由電子散射的康普頓效應法等。另一大類方法則是利用非鐵磁性金屬的物理性質在磁場中的變化來反映費密面的結構。其中德哈斯-范阿耳芬效應法測量晶體的磁化率隨磁場強度的單調增長而發生的振蕩式變化。舒布尼科夫-德哈斯效應法測量晶體電阻率隨磁場增強的振蕩式變化;磁聲效應法測量超聲波在晶體中的衰減隨磁場增強的變化;迴旋共振法測量晶體的微波阻抗的振蕩式變化;而磁熱效應法則是測量放在磁場中的絕熱晶體樣品的溫度隨磁場增強而發生的振蕩式變化,這裡只對第二大類方法的基本原理作一個簡要的介紹。電子在磁場中受到洛倫茲力的作用而發生迴旋運動。作迴旋運動的電子的能量不變化,所以它在k空間的代表點的運動軌跡是等能面與垂直於磁場 B的平面相交的截線。由量子力學的基本原理可以證明,這個軌道在與B垂直的平面上的截面積Sn是量子化的:式中n是整數,An是軌道在與 B垂直的平面上的投影的截面積(指在坐標空間的軌道),γ是一個常數。如果費密面在與磁場 B垂直的平面上的截線所決定的軌道面積極值為Sext,那麼,每當磁場
實驗測定方法 利用大型計算機已經可以相當精確地決定實際金屬的費密面。也建立了許多有效的實驗方法。A.P.皮帕德是第一個成功地從實驗上測定金屬的費密面的,他利用了金屬的反常趨膚效應。當金屬受到微波照射時,由於趨膚效應,微波電場只存在於表面附近很薄一層內。如果這塊金屬是純凈的單晶,電子自由程 l大於趨膚層的深度 ξ。費密面上不同速度的電子和微波電場的作用會不同, 當l≥ξ時,這實際上相當於“切”下費密面上速度近似平行於表面的部分。所以,測量各種情況下的表面阻抗,可以獲得費密面的信息。皮帕德就用這辦法得到了銅的費密面。隨後又發展了許多其他方法。常用的方法可以分為兩大類。一大類是與碰撞效應有關的方法。例如探測正電子與金屬中自由電子湮沒時發射的光子的動量分佈的湮沒效應法,測量X 射線被金屬中自由電子散射的康普頓效應法等。另一大類方法則是利用非鐵磁性金屬的物理性質在磁場中的變化來反映費密面的結構。其中德哈斯-范阿耳芬效應法測量晶體的磁化率隨磁場強度的單調增長而發生的振蕩式變化。舒布尼科夫-德哈斯效應法測量晶體電阻率隨磁場增強的振蕩式變化;磁聲效應法測量超聲波在晶體中的衰減隨磁場增強的變化;迴旋共振法測量晶體的微波阻抗的振蕩式變化;而磁熱效應法則是測量放在磁場中的絕熱晶體樣品的溫度隨磁場增強而發生的振蕩式變化,這裡只對第二大類方法的基本原理作一個簡要的介紹。電子在磁場中受到洛倫茲力的作用而發生迴旋運動。作迴旋運動的電子的能量不變化,所以它在k空間的代表點的運動軌跡是等能面與垂直於磁場 B的平面相交的截線。由量子力學的基本原理可以證明,這個軌道在與B垂直的平面上的截面積Sn是量子化的:式中n是整數,An是軌道在與 B垂直的平面上的投影的截面積(指在坐標空間的軌道),γ是一個常數。如果費密面在與磁場 B垂直的平面上的截線所決定的軌道面積極值為Sext,那麼,每當磁場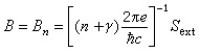 (6)時,就有一個容許的迴旋軌道Sn與這個費密面上的極值軌道相重合。當磁場B由零逐漸增加時,這種情況周期地出現。所以與金屬費密面相關聯的物理性質,如磁化率、電阻率等也就隨磁場強度發生振蕩式變化。由式(6)可見,相鄰兩個磁場值Bn與Bn+1之間,滿足關係式
(6)時,就有一個容許的迴旋軌道Sn與這個費密面上的極值軌道相重合。當磁場B由零逐漸增加時,這種情況周期地出現。所以與金屬費密面相關聯的物理性質,如磁化率、電阻率等也就隨磁場強度發生振蕩式變化。由式(6)可見,相鄰兩個磁場值Bn與Bn+1之間,滿足關係式 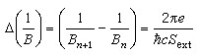 , (7)所以可從這些量變化的周期直接測定費密面在與磁場垂直的平面上的投影。使磁場沿晶體的不同取向進行一系列的測量,就可得出關於整個費密面的知識。進行這類實驗要保證電子在磁場中作迴旋運動基本上不被散射擾亂。如用 τ表示電子漂移運動的弛豫時間(它由散射決定),用ωc表示在磁場中的電子迴旋頻率,則要求滿足基本條件
, (7)所以可從這些量變化的周期直接測定費密面在與磁場垂直的平面上的投影。使磁場沿晶體的不同取向進行一系列的測量,就可得出關於整個費密面的知識。進行這類實驗要保證電子在磁場中作迴旋運動基本上不被散射擾亂。如用 τ表示電子漂移運動的弛豫時間(它由散射決定),用ωc表示在磁場中的電子迴旋頻率,則要求滿足基本條件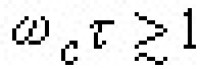 。 (8)因此這類實驗一般需要有較純的樣品,並在低溫下進行,同時還需要較強的磁場B。配圖相關連接
。 (8)因此這類實驗一般需要有較純的樣品,並在低溫下進行,同時還需要較強的磁場B。配圖相關連接

費密面
費密面
費密面
費密面
費密面

費密面
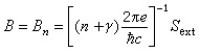
費密面
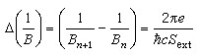
費密面
費密面