失真函數
失真函數
在實際問題中,信號有一定的失真是可以容忍的。但是當失真大於某一限度后,信息質量將被嚴重損傷,甚至喪失其實際價值。要規定失真限度,必須先有一個定量的失真測度。
失真函數是人們根據實際需要和失真引起的損失、風險、主觀感覺上的差別大小等因素人為規定的。
人的視覺、聽覺等對信號的失真有一定的容忍度。然後人們就用失真函數表示失真程度。用信息率失真函數表示在某種程度的失真情形下信源的熵。
當a=b,d(ab)=0;
當a≠b,d(ab)=α(α>0);
如果a=b,i=1,2,…,n,j=1,2,…,則沒有失真。
如果a≠b,就產生了失真。
失真的大小,用一個量來表示,即失真函數d(a,b),以衡量用b代替a所引起的失真程度。
常用失真函數及其適用性
失真函數比較
均方誤差失真和絕對誤差失真只與(a–b)有關,而不是分別與a及b有關,在數學處理上比較方便。
相對誤差失真與主觀特性比較匹配,因為主觀感覺往往與客觀量的對數成正比,但在數學處理中就要困難得多。
其實選擇一個合適的、完全與主觀特性匹配的失真函數是非常困難的,更不用說還要易於數學處理。當然不同的信源應有較好的失真函數,所以在實際問題中還可以提出許多其他形式的失真函數。
平均誤差失真是信源統計特性,通道統計特性和失真度的函數,當以上三個量p(a),p(b∕a),p(a,b)給定后,平均失真度就不再是一個隨機量了,而變成一個確定的量。人們所允許的壓縮失真都是平均意義上的失真。
平均失真由信源分佈p(a)、通道的轉移概率p(b∕a)和失真函數d(a,b)決定,若p(a)和d(a,b)已定,則調整p(b∕a)使平均失真度小於或等於D。
D為失真許可的試驗通道。
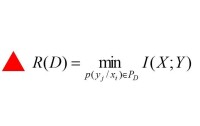
信息率失真函數
失真在傳輸中是不可避免的。連續信源輸出的信息量為無窮大,不可能實現無失真信源編碼。接收者(信宿)無論是人還是機器設備,都有一定的分辨能力與 靈敏度,超過分辨能力與靈敏度的信息傳送過程是毫無意義的。即使信宿能分辨、能判別,但對通信質量的影響不大,也可以稱它為允許範圍內的失真。如果R>C,就必須對信源壓縮,使得壓縮后的R*
綜上所述,一般可以對信源輸出的信息進行限失真處理,降低信息率,提高傳輸效率。
目錄
