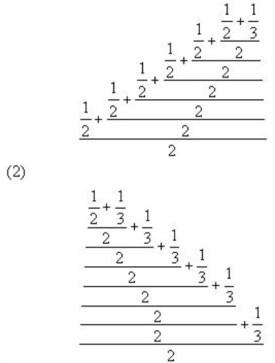
繁分數
分數形式的數
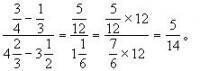
繁分數
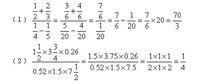
繁分數

繁分數
一、繁分數是分數形式的數,但不是分數
數叫做分數。定義中的“形”是指分子、分母和分數線構成了分數的“形”。m和n都是整數,且n≠0是指分子、分母的取值範圍,兩者有機地結合,構成了分數的整體,全面地揭示了分數的內涵,同時也確定了分數的全部外延。
和主分數線,這三部分構成了繁分數的“形”。這和分數的“形”是類似的。我們可以說繁分數是分數形式的數。但是,繁分數的分子部分分母部分含有分數,或分子部分分母部分都含有分數,這和分數的分子分母比,取值範圍擴大了,和分數的定義相悖,所以繁分數不是分數,也不是什麼特殊的分數。
二、繁分數是數,而不是除法式子
一個有意義的除法算式應包括定義範圍內的被除數、除數和除號,它是一種運算表達形式。只有通過運算后,才能得出一個商數來,所以除法算式和一個數是兩回事。
三、繁分數定義的表述
根據繁分數的特點和內涵,考慮到既有分數的“形”,又有分子部分分母部分含有分數的特殊情況,它的定義可以這樣表述:如分數形式,分子或分母含有分數,或分子與分母都含有分數的數,叫繁分數。
在一個繁分數里,最長的分數線叫做繁分數的主分數線,主分數線上下不管有多少個數或運算,都把它們分別看作是繁分數的分子和分母。
把繁分數化為最簡分數或整數的過程,叫做繁分數的化簡。
繁分數的化簡一般採用以下四種方法:
(1)往上翻
先找出主分數線,確定分子部分和分母部分,然後這兩部分分別進行計算,每部分的計算結果能約分的要約分,最後改成“分子部分÷分母部分”的形式,再求出結果。
(2)擴倍數
繁分數化簡的另一種方法是:根據分數的基本性質,經繁分數的分子部分和分母部分同時擴大相同的倍數(這個倍數必須是分子部分與分母部分所有分母的最小公倍數),從而去掉分子部分和分母部分的分母,然後通過計算化為最簡分數或整數。
(3)逐步法
繁分數的化簡一般由下至上,由左到右,逐次進行化簡。
繁分數的分子部分和分母部分有時也出現是小數的情況,如果是分數和小數混合出現的形式,可按照分數、小數四則混合運算的方法進行處理。即:把小數化成分數,或把分數化成小數后再進行化簡。
當分子部分和分母部分都統一成小數后,化簡的方法是:中間約分時,把小數看成整數,但要注意小數點不要點錯位置。
也可以根據分數的基本性質,把繁分數的分子部分和分母部分都變成整數連乘,然後交叉約分算出結果來。
(4)拆分法
利用整數的運算性質進行化簡,通常可用拆分法或找規律法。
拆分法:
此題可用拆分法解決,把2002×2003拆成2001×2003+2003,即可簡便計算。
解:原式
找規律法:
其實此題也用到了拆分法,把分子算出來,得36,再拆分成6×6。對於分母較大的數,可找規律。
即
所以這裡的分母。這樣即可簡便計算。
繁分數的教學在數學教學中是難點之一。通過教學主要使學生掌握以下幾方面的知識:
一、要使學生懂得繁分數的意義;
二、要使學生知道主分數線上下的數不管怎樣複雜,上面的數都是分子,下面的數都是分母,牢記繁分數本身是一個分數;
三、掌握繁分數化簡的方法,並懂得利用分數與除法的關係,可以把繁分數改寫成四則混合算式,從而了解分數線還起著括弧的作用。教學時要引導學生從理解繁分數的概念入手,然後講清繁分數化簡的幾種方法,這是教這部分內容的關鍵。
最新版的小學數學教材已不需要學習繁分數,學習分數除法時是直接用簡分數進行計算。