積空間

拓撲學和數學的相關領域中，積空間是指一族拓撲空間的卡積，並配備了一個稱為積拓撲的自然的拓撲結構。

令I為（可能無窮的）指標集並設Xi對於每個I中的i為一個拓撲空間。置X = Π Xi，也即集合Xi的卡積。對於每個I中的i，我們有一個標準投影pi : X → Xi。X上的積拓撲定義為所有投影pi在該拓撲下連續的最疏拓撲（也就是開集最少的拓撲）。該乘積拓撲有時也稱為吉洪諾夫拓撲。

很明顯，X上的乘積拓撲可以表述為形為pi(U)的集合生成的拓撲，其中i屬於I而U是Xi的一個開集。換句話說，集合{pi(U)}構成X上的拓撲的子基。X的子集是開的當且僅當它是(可能無窮多的)的有限個形為pi(U)的集合的交集的並集。pi(U)有時稱為開柱，而它們的交集稱為柱集。

我們可以用構成X的空間Xi的基來表述乘積拓撲的基。設對於每個i屬於I，選取一個集合Yi或者是整空間Xi或者是該空間的一個基，並且滿足Xi = Yi對於除了有限個I中的i之外的所有i成立。令B為集合Yi的卡積。所有可以這樣構造的B集合的族構成乘積空間的一個基。這意味著有限多空間的乘積有一個由Xi的基元素的乘積組成的基。

如果指標集為有限（特別是，對於兩個拓撲空間的乘積），則積拓撲有更簡單的表述。這個情況下，每個Xi的拓撲的乘積構成X上的拓撲的一個基。一般來講，Xi的拓撲的乘積構成一個稱為X上的盒拓撲的基。一般情況下，盒拓撲比積拓撲更細，但是對於有限乘積，它們是相同的。

從實直線R上的標準拓撲開始，定義n份R的乘積，就得到普通的R上的歐幾里得拓撲。

康托爾集同胚於可數個離散空間{0,1}的乘積而無理數的空間同胚於可數個自然數集的乘積，每個集合也是採用離散拓撲。

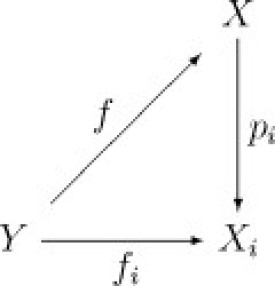
乘積空間X加上標準投影，可以用如下的泛性質來刻劃：若Y是拓撲空間，並且對於每個I中的i，fi : Y → Xi是一個連續映射，則存在恰好一個連續映射f : Y → X滿足對於每個I中的i如下交換圖成立：

這表明乘積空間是拓撲空間範疇中的積。從上述范性質可以得出映射f : Y → X連續當且僅當fi = pi o f對於所有I中的i連續。在很多情況下，檢查分量函數fi的連續性更為方便。檢驗映射g : X→ Z是否連續通常更難；可以試著用某種方式利用pi連續這一點。

除了連續，標準投影pi : X → Xi也是開映射。這表示每個積空間的開子集投影到Xi上還是開集。反過來不真：若W是到所有Xi的投影都是開集的積空間的子空間，則W不一定是X中的開集。（例如，W = R \ (0,1).）標準投影通常不是閉映射。

積拓撲有時稱為點式收斂拓撲，因為：X上的一個序列（或者網）收斂當且僅當它所有到當且僅當所有Xi收斂。特別是，如果考慮所有在空間X = R對於所有I上的實值函數，在積拓撲上的收斂就是函數的點式收斂。

積拓撲的一個重要定理就是吉洪諾夫定理：任何緊緻空間的乘積是緊緻的。對於有限乘積很容易看出，而其一般情況等價於選擇公理。

可分離性 每個T0空間的積是T0的。每個T1空間的積是T1的。每個豪斯多夫空間的積是豪斯多夫的。每個正則空間的積是正則的。每個吉洪諾夫空間的積是吉洪諾夫空間。正規空間的積不一定是正規的。緊緻性 每個緊緻空間的積是緊緻的（吉洪諾夫定理）局部緊緻空間的積不一定是局部緊緻的。連通性 每個連通（路徑－連通）空間是連通的（路徑－連通的）。每個遺傳性不連通空間的積是遺傳性不連通的。每個"局部看起來"一個標準投影F × U → U的空間稱為纖維叢。