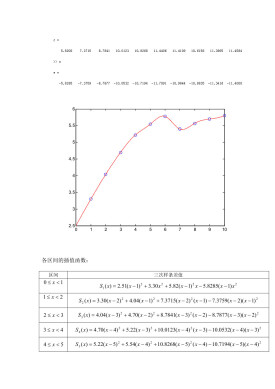
三次插值法

三次插值法

三次插值法(cubic interpolation method)是一種多項式插值法，逐次以三次曲線φ(t)=a0+a1t+a2t+a3t的極小點逼近尋求函數f(t)的極小點的一種方法。具體做法是：設t1

目錄

1基本介紹 2相關分析

基本介紹

三次插值法是在1959年由Davidon首先提出來的，它是用三次插值逼近，而求的近似最小點的一種迭代演演算法。

二次多項式逼近法也稱拋物線法，它的原理是利用三個函數值來構造一個二次多項式逼近原來的函數。當函數的導數不難求得時，可以利用兩個點處的函數與導數來構造三次多項式逼近原來的函數。

為了保證極小點在給定區間的內部，要求函數在a點的右邊下降，而在b點的右邊上升。如果用a、b兩點的導數表示，即

且

其幾何意義如圖1所示。

·

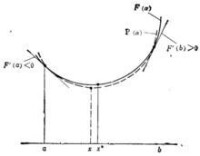
圖1

相關分析

設三次多項式的一般形式為

其中是四個待定係數，它可由a、b兩點的函數值及其一階導數列出四個方程式，則可求得四個係數值。因為

若步長從a點計算起，即，由此可得：

又若，得

聯立解(3)～(6)式得出：

現要求在內的極小點作為原目標函數F(x)的極小點的一個近似，為此要求出方程：

在內的根，並根據極小點的充分條件，在此根處應有二階導數大於零，即

式(11)的兩個根

將式(13)代入式(12)，得

因為是求極小值，故根前應取正號，變換(13)式為：

三次插值法

得

當時，是二次插值的情況；如，則是三次插值。

目錄