黏著空間
黏著空間
的一個子空間。黏著空間的一個通常例子是當 是一個帶有一個點的空間則黏著空間是
在數學中,粘著空間(adjunction space)是拓撲學中一個常見構造,它將一個拓撲空間貼或“黏合”到另一個。具體地,設X 與Y 是一個拓撲空間以及Y 的一個子空間。設 是一個連續映射(稱為 貼映射,attaching map)。黏著空間 之構造如下:先取X 與Y 的不交並然後對所有x 屬於A,然後將x 與f(x) 等化。用數學符號表示為:
有時黏著空間也寫成 。在直覺上,我們認為Y 通過映射f 黏合到X。
作為一個集合, 由X 與 的不交並組成;但其拓撲由商構造確定。當A 是Y 的一個閉子集時,可以證明映射 時一個閉嵌入且 是一個開嵌入。
黏著空間的一個通常例子是當Y 是個閉n-球(或胞腔)而A 是球的邊界,即-球面。歸納地將胞腔沿著它們的球面邊界貼到這些空間得到了一個 CW-復形的例子。黏著空間也用於定義流形的連通和。這裡我們首先將X 與Y 各自挖掉一個開球,然後將挖去球的X 與Y 沿著挖去球剩下的邊界沿著一個貼映射黏合。如果A 是一個帶有一個點的空間則黏著空間是X 與Y 的楔和(wedge sum)。如果X 是一個帶有一個點的空間則粘著空間是商。
黏著構造是拓撲空間範疇中推出的例子。這就是說,黏著空間是關於如下交換圖表的泛對象:
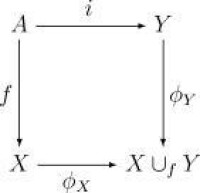
黏著空間
