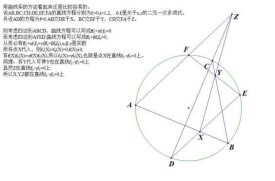
帕斯卡定理
帕斯卡定理
帕斯卡定理指圓錐曲線內接六邊形（包括退化的六邊形）其三對邊的交點共線，與布列安桑定理對偶，是帕普斯定理的推廣。定理約於公元1639年為法國數學家布萊士·帕斯卡所發現，被稱為帕斯卡定理，是射影幾何中的一個重要定理。
如果一個六邊形內接於一條二次曲線(圓、橢圓、雙曲線、拋物線)，那麼它的三對對邊的交點在同一條直線上。
由於六邊形的存在多種情況，帕斯卡定理的圖形也存在多種，它們雖然看起來截然不同，但均為帕斯卡定理，證明它們的方法也是相同的
可以利用射影變換，將圓錐曲線的命題轉化為圓的命題
現在只需要證明圓的內接六邊形三雙對邊的交點共線即可
帕斯卡定理的證法有許多種，在此只列舉三種
面積法：
面積法
連接，設交於(如圖1)，交於(如圖2)
要證共線，只需證交於一點。
現在只需證：，即證：
共邊定理+公交定理可得：
命題得證
梅涅勞斯定理證法：
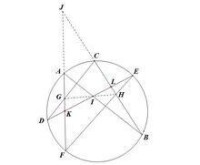
梅涅勞斯定理證法
對和截線分別應用梅涅勞斯定理得：
三式相乘得：
圓冪定理得：
將(2),(3),(4)式代入(1)得：
梅涅勞斯逆定理得：共線，命題得證
位似證法：
作外接圓交于于
∵，∴
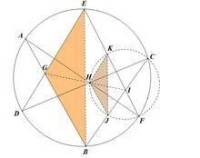
位似證法
∴與位似
又位似三角形對應點的所在的直線交於一點
即交於一點，此點為
∴共線，命題得證
角元賽瓦定理證法
利用角元賽瓦定理逆定理證明共點（下面推導省去符號）
我們有
（第二步為對用角元賽瓦定理）
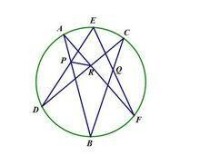
塞瓦定理（角元）證法
射影證法
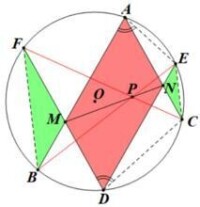
射影證法
在異於題設所在平面的空間上任取一點作為射影中心，將射影為一對平行直線；將射影為一對平行直線，再將中心射影後圖形中的橢圓仿射為圓（如右圖）
則由平行四邊形及同弧圓周角性質知，則根據同圓內等弦長對應等圓周角推導知則觀察圖中兩個綠色三角形笛沙格定理（逆）知則帕斯卡定理得證。
基本信息
- 中文名
- 帕斯卡定理
- 外文名
- Pascal's theorem
- 應用學科
- 數學
- 適用領域
- 射影幾何
- 提出時間
- 公元1639年
- 提出者
- 帕斯卡
- 表達式
- BG∩EH=Q∈PR