洛倫茲因子
洛倫茲因子
洛倫茲因子又稱相對論因子,是洛倫茲為了解釋邁克爾孫-莫雷實驗的光速不變結論,設想,觀察者相對於以太以一定速度運動時,長度在運動方向上發生收縮的觀點而推導出來的靜系長度與動系長度之比的洛倫茲因子,但是他認為這沒有物理意義,把它當作純數學處理。而愛因斯坦就不一樣了,他詳細說明了它的物理意義是動系對比靜系發生”尺縮“和”鐘慢“的係數。
洛倫茲為了解釋邁克爾孫-莫雷實驗的光速不變結論,設想,觀察者相對於以太以一定速度運動時,長度在運動方向上發生收縮的觀點而推導出來的靜系長度與動系長度之比的洛倫茲因子,但是他認為這沒有物理意義,把它當作純數學處理。而愛因斯坦在1905年發表的題為 《論動體的電動力學》的論文,提出狹義相對論的基本理論。
• 光速最大:任何運動物體的不可以超過光速
• 尺縮:運動物體在運動方向的尺寸相對靜止時縮短
• 鐘慢:運動物體所在時空相對靜止時空時間流逝更慢
狹義相對論給出的動系相對於靜系的”尺縮“”鐘慢“的比例因子即 洛倫茲因子,表達為:
其中c為真空光速,v為動系相對靜系的移動速度。
動系中物體運動方向的尺寸讀數為:,L為靜系的尺寸
動系中的時間讀數為: ,t 為靜系的時間
基於洛倫茲因子的產生式光速恆定的假設。
即一束光線在任意參照系,對任意觀察者,速度一樣都為c。
因此可以考察現實中類似的情況:
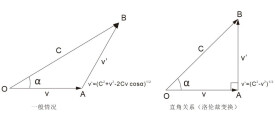
• 相對於原點O,動點A和B分別以速度v和c,離開O點,速度加角為α,則B對A的相對速度為v’
• 求A、O兩點測得B速率一樣的變換方法
由矢量疊加的平行四邊形法則、餘弦定理,可得v’,如圖所示。
則有變換因子
以OB為標準,有兩個方案:(二選一)
改變測量AB距離的尺的讀數,都乘以β(尺縮);
改變測量AB時間的鐘的讀數,都除以β(鐘慢)。
這樣就能計算出
• 特殊情況:上述速度與夾角構成直角關係
可得 ,即相對論中“尺縮”、“鐘慢”的核心:洛倫茲因子
可以看到,選擇直角關係,可以消除α的出現。(使得洛倫茲變換的結果只與V和C有關,更具普遍性。)
• 得到啟示:
在兩邊和夾角確定時,三角形具有惟一性,可得
如果洛倫茲變換就是上述疊加關係,則
洛倫茲變換隻能在動系原點有現實三維空間的解,是一個二維平面
洛倫茲變換隻對特殊角度的光線有現實三維空間的解
洛倫茲變換不能對任一點完成有物理意義的變換
通過洛倫茲變換無法構成一個現實三維的物理空間
在現實中變換因子用於改變尺鐘的讀數,並不是時間和長度真的發生變化。
現實中的變換尺縮和鐘慢只選一個即可,而相對論認為兩者同時具備。