幾何變換

在幾何的解題中，當題目給出的條件顯得不夠或者不明顯時，我們可以將圖形作一定的變換，這樣將有利於發現問題的隱含條件，抓住問題的關鍵和實質，使問題得以突破，找到滿意的解答．圖形變換是一種重要的思想方法，它是一種以變化的、運動的觀點來處理孤立的、離散的問題的思想，很好地領會這種解題的思想實質，並能準確合理地使用，在解題中會收到奇效，也將有效地提高思維品質．

初中圖形變換包含平移、翻折和旋轉，我們要通過實驗、操作、觀察和想象的方法掌握運動的本質，在圖形的運動中找到不變數，然後解決問題。

幾何變換是建立在集合的變換與映射基礎上的。

設T是平面pai的一個變換，F是平面上的一個圖形（即平面的一個子集），令

那麼，圖形F'稱為圖形F在變換T下的像,T是一個幾何變換。

如果平面上一個點A滿足,那麼A稱為T的不動點；如果圖形F滿足那麼F是T的不變圖形。

如果對於平面上任意兩點A,B與其象點總有那麼稱T為合同變換

如果存在一個常數k，使,那麼稱T為相似變換，k為相似係數或相似比

保持角的方向不變的相似變換為真正相似變換，角的方向相反的為鏡像相似變換。

兩圖形真正相似也稱順相似或同向相似，鏡像相似也稱逆相似。

內容提要：翻折變換是平面到自身的變換，若存在一條直線l，使對於平面上的每一點P及其對應點P′，其連線PP′都被定直線l垂直平分，則稱這種變換為翻折變換，定直線l稱為對稱軸．翻折變換有如下性質：

(1)把圖形變為與之全等的圖形；

(2)關於l對稱的兩點連線被l垂直平分．

證題過程中使用翻折變換，可保留原有圖形的性質，且使原來分散條件相對集中，以利於問題的解決．

內容提要：平移變換是平面到自身的變換，將平面上任一點P變換到P′，使得：(1)射線PP′有給定的方向；(2)線段PP′有給定的長度．則稱這種變換為平移變換．在平移變換下，圖形變為與之全等的圖形，直線變為與之平行的直線．

在解幾何問題時，常利用平移變換使分散的條件集中在一起，具有更緊湊的位置關係或變換成更簡單的基本圖形．

內容提要：旋轉變換是平面到它自身的變換，使原點O變換到它自身，其他任何點X變到X′，使得：(1)；(2)．則稱這樣的變換為旋轉變換，O稱為旋轉中心．旋轉變換保持圖形全等，但圖形方位可能有變化．在幾何解題中，旋轉的作用是使原有圖形的性質得以保持，但改變其位置，使能組合成新的有利論證的圖形．

一、平移變換

1．　定義 設是一條給定的有向線段，T是平面上的一個變換，它把平面圖形F上任一點X變到X‘，使得=，則T叫做沿有向線段的平移變換。記為XX’，圖形FF‘ 。

2．　主要性質 在平移變換下，對應線段平行且相等，直線變為直線，三角形變為三角形，圓變為圓。兩對應點連線段與給定的有向線段平行（共線）且相等。

二、軸對稱變換

1．　定義 設l是一條給定的直線，S是平面上的一個變換，它把平面圖形F上任一點X變到X’，使得X與X‘關於直線l對稱，則S叫做以l為對稱軸的軸對稱變換。記為XX’，圖形FF‘ 。

2．　主要性質 在軸對稱變換下，對應線段相等，對應直線（段）或者平行，或者交於對稱軸，且這兩條直線的夾角被對稱軸平分。

三、旋轉變換

1．　定義 設α是一個定角，O是一個定點，R是平面上的一個變換，它把點O仍變到O（不動點），而把平面圖形F上任一點X變到X’，使得，且，則R叫做繞中心O，旋轉角為α的旋轉變換。記為XX‘，圖形FF’ 。

其中時，表示的始邊OX到終邊OX’的旋轉方向為順時針方向；時，為逆時針方向。

2． 主要性質 在旋轉變換下，對應線段相等，對應直線的夾角等於旋轉角。

四、位似變換

1．　定義 設O是一個定點，H是平面上的一個變換，它把平面圖形F上任一點X變到X‘，使得 =k·，則H叫做以O為位似中心，k為位似比的位似變換。記為XX’，圖形FF‘ 。

其中k>0時，X’在射線OX上，此時的位似變換叫做外位似；時, X‘在射線OX的反向延長線上，此時的位似變換叫做內位似。

2．　主要性質 在位似變換下，一對位似對應點與位似中心共線；一條線上的點變到一條線上，且保持順序，即共線點變為共線點，共點線變為共點線；對應線段的比等於位似比的絕對值，對應圖形面積的比等於位似比的平方；不經過位似中心的對應線段平行，即一直線變為與它平行的直線；任何兩條直線的平行、相交位置關係保持不變；圓變為圓，且兩圓心為對應點；兩對應圓相切時切點為位似中心。

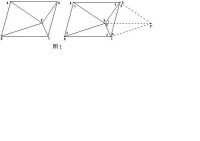
【例1】P是平行四邊形ABCD內一點，且。

求證：

【分析】作變換

則。由都是平行四邊形，知。由已知，得。

四點共圓。故

【例2】“風平三角形”中，

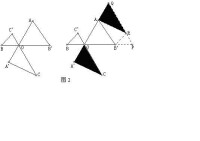
求證：

【分析】作變換，則R’、R‘’重合，記為共線，共線，共線，為等邊三角形。

【例3】在兩條對角線長度以及夾角一定的所有凸四邊形中，試求周長最小的四邊形。

【分析】取AC、BD的中點E、F，令，則是一個符合條件的平行四邊形。延長。

∵E是AC的中點且分別為的中點。

同理可得

故當四邊形為平行四邊形時，周長最小。

【評註】當已知條件分散，尤其是相等的條件分散，而又不容易找出證明途徑，或題目中有平行條件時，將圖形的某一部分施行平移變換，常常十分湊效。

【例4】P是的弦AB的中點，過P點引的兩弦CD、EF，連結DE交AB於M，連結CF交AB於N。求證：。（蝴蝶定理）

【分析】設GH為過P的直徑，FF’F，顯然。又，

又

，四點共圓。

【評註】一般結論為：已知半徑為R的內一弦AB上的一點P，過P作兩條相交弦，連交AB於，已知，P到AB中點的距離為a，則。（解析法證明：利用二次曲線系知識）

【例5】是給定銳角內一個定圓，試在及射線上各求一點使得的周長為最小。

【分析】在圓O上任取一點P0，令，連結分別交。顯然是在取定P0的情況下周長最小的三角形。

設交CA於E，交CB於F，則

∵四點共圓，CP0是該圓直徑，由正弦定理，

∴當CP0取最小值時，EF為最小，從而△P0Q1R1的周長為最小，於是有作法：

連結OC，交圓周於P，令，連結分別交。則P、Q、R為所求。

【例6】是它的任一內接三角形。求證：

【分析】設。則

又，A點在線段P‘P’‘上或在凸四邊形的內部。

【評註】如果題設中有角平分線、垂線，或圖形是等腰三角形、圓等軸對稱圖形，可以將圖形或其部分進行軸對稱變換。此外，也可以適當選擇對稱軸將一些線段的位置變更，以便於比較它們之間的大小。

【例7】以的邊為斜邊分別向外作等腰直角三角形，M是BC的中點。求證：

【分析】延長BP到E，使，延長CQ到F，使，則都是等腰三角形。

顯然：

而

【例8】已知O是內一點，P是內任一點，求證：

【分析】將連結。則都是正三角形。

。顯然

由於四點共線。

【例9】的三邊分別交於點過上述六點分別作所在邊的垂線，設三線相交於一點D。求證：三線也相交於一點。

【分析】關於圓心O成中心對稱，

同理，

的公共點D在變換下的像D’也是像的公共點，即三線也相交於一點。

【例10】的外接圓O的直徑，過D作的切線交BC於P，連結並延長PO分別交AB、AC於M、N。求證：。

【分析】設，而MB，

三點共線，三點共線，且。

取BC中點G，連結

四點共圓。

，而由

四點共圓。

而G是BC的中點，