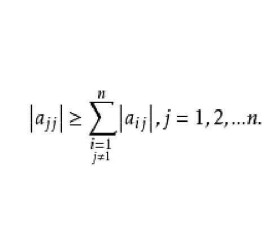對角優勢矩陣
對角優勢矩陣
對角優勢矩陣是一類特殊的方陣，複數域上的m×m矩陣A，如果它的的第一行主對角線元素的模均不小於非主對角線元素模之和則稱A為對角優勢矩陣。第i行非對角元素的模之和稱為第i行的行估計或行半徑，第i列非對角元素的模之和稱為第i列的列估計或列半徑。若矩陣A既為行對角優勢矩陣，又為列對角優勢矩陣，則稱A是對角優勢矩陣。行(列)對角優勢矩陣必為非奇異矩陣，且其逆矩陣的各對角元素的模在同列(行)中為最大，如果控制系統的開環傳遞函數矩陣在虛軸和無窮大半徑組成的包圍整個右半複平面的閉合曲線上處處有行(列)對角優勢矩陣，則閉環系統穩定性可以僅根據其對角元素進行判斷。
定義1 如果n階矩陣A的第一列主對角線元素絕對值均不小於非主對角線元素絕對值之和，即
則稱A為 對角優勢矩陣。
定義2 如果A的每一列主對角線元素絕對值均大於非主對角線元素絕對值之和
那麼稱A為 嚴格對角優勢矩陣。
定義3 如果A為不可分的對角優勢矩陣，且至少有一列其主對角線元素絕對值嚴格大於非主對角線元素絕對值之和，那麼稱A為 不可分對角優勢矩陣。
以上定義都是對列而言的，類似地可以對行來定義。
例1 給定矩陣
由於
因此A為嚴格對角優勢矩陣。
如果n階矩陣 為嚴格對角優勢矩陣，那麼 A是可逆的。
設n階矩陣 的主對角線元素為正實數，即，且具有嚴格對角優勢，則 A的所有特徵值 的實部為正。
證明 用反證法證明。假設存在 A的一個特徵值，其實部為非正，根據 A的嚴格對角優勢性及其主對角線元素大於零，則有
這表明矩陣 具有嚴格對角優勢，根據定理1知，即 不是 A的特徵值，這與 是 A的特徵值矛盾，所以證明了定理的論斷。
設 為n階非負矩陣，其主對角線元素都小於1，如果矩陣為嚴格對角優勢矩陣，則 A的任一特徵值 的絕對值小於1，即。
給定線性方程組，其中矩陣 的主對角線元素為正，即，而非主對角線元素非正，即，且 A為嚴格對角優勢矩陣，如果 ，則該方程組有非負解，即 。
例2 給定
由於 A的主對角線元素大於零，而非主對角線元素為非正數，且具有嚴格對角優勢以及，因此方程組 具有非負解，事實上
這裡給出關於不可分對角優勢矩陣的四個定理。
若 A為n階不可分對角優勢矩陣，則 A是可逆的。
若A為n階不可分對角優勢矩陣，且 A的所有主對角線元素為正實數，則 A的所有特徵值 的實部為正。
設 為n階非負矩陣，且主對角線元素都小於1，如果矩陣為不可分對角優勢矩陣，則 A的任一特徵值 的絕對值小於1，即。
給定線性方程組 ，其中n階矩陣 的主對角線元素為正，即，而非主對角線元素非正，即 ,且A為不可分對角優勢矩陣。如果 ,則該方程組有非負解。
這些定理在分析線性經濟模型及其穩定性時具有重要的應用。
基本信息
- 外文名
- diagonallydominantmatrix
- 所屬學科
- 數理科學