獵鹿博弈
獵鹿博弈
獵鹿博弈(Stag Hunt Game, SHG)又稱獵鹿模型(Stag Hunt Model)、獵人的帕累托效率、安全博弈(Assurance Game)、協調博弈(Coordination Game),對應於信任困境(Trust Dilemma)。其源自法國啟蒙思想家盧梭(Jean-Jacques Rousseau)的著作《論人類不平等的起源和基礎》中的一個故事。兩個人出去打獵,獵物為鹿和兔,他們互不知道對方選擇的獵物。如果選擇鹿,則需要另一人也選擇鹿,產生合作才能成功狩獵。而選擇兔為獵物,不需要合作也能成功,但是獵兔的收益要小於獵鹿。
區別於囚徒困境(Prisoner's Dilemma, PD),SHG有兩種純策略納什均衡:全合作或全背叛,而在PD中,儘管全合作是帕累托最優,但只有全背叛才能達到納什均衡。
獵鹿博弈又稱 獵鹿模型(Stag Hunt Model)、獵人的帕累托效率,源自啟蒙思想家盧梭的著作《論人類不平等的起源和基礎》中的一個故事。
古代的村莊有兩個獵人。當地的獵物主要有兩種:鹿和兔子。如果一個獵人單兵優作戰,一天最多只能打到4隻兔子。只有兩個一起去才能獵獲一隻鹿。從填飽肚子的角度來說,4隻兔子能保證一個人4天不挨餓,而一隻鹿卻能讓兩個人吃上10天。這樣兩個人的行為決策可以形成兩個博弈結局:分別打兔子,每人得4;合作,每人得10。這樣獵鹿博弈有兩個納什均衡點,那就是:要麼分別打兔子,每人吃飽4天;要麼合作,每人吃飽10天。
這裡不妨假設兩個獵人叫A和B。我們引入一種矩陣式的對兩人博弈的描述方法,見下圖:
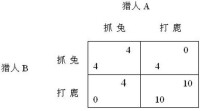
獵鹿博弈.jpg
在獵鹿博弈中,根據納什均衡的定義,應用博弈論中的“嚴格劣勢刪除法”可以得到該博弈有兩個納什均衡點,那就是:要麼分別打兔子,每人吃飽4天;要麼合作,每人吃飽10天。
兩個納什均衡,就是兩個可能的結局。兩種結局到底哪一個最終發生,這無法用納什均衡本身來確定。比較[10,10]和[4,4]兩個納什均衡,明顯的事實是,兩人一起去獵鹿比各自去抓兔子可以讓每個人多吃6天。按照經濟學的說法,合作獵鹿的納什均衡比分頭抓打兔子的納什均衡具有帕累托優勢。與[4,4]相比,[10,10]不僅有整體福利改進,而且每個人都得到福利改進。換一種更加嚴密的說法就是,[10,10]與[4,4]相比,其中一方收益增大,而其它各方的境況都不受損害。這就是[10,10]對於[4,4]具有帕累托優勢的含義。
在經濟學中,帕累托效率準則是:經濟的效率體現於配置社會資源以改善人們的境況,主要看資源是否已經被充分利用。如果資源已經被充分利用,要想再改善我就必須損害你或別的什麼人,要想再改善你就必須損害另外某個人,一句話,要想再改善任何人都必須損害別的人了,這時候就說一個經濟已經實現了帕累托效率。相反,如果還可以在不損害別人的情況下改善任何人,就認為經濟資源尚未充分利用,就不能說已經達到帕累托效率。
目前在世界上比比皆是的企業強強聯合就很接近於獵鹿博弈的帕累托改善,跨國汽車公司的聯合、日本兩大銀行的聯合等等均屬此列,這種強強聯合造成的結果是資金雄厚、生產技術先進、在世界上佔有的競爭地位更優越,發揮的影響更顯赫。總之,他們將蛋糕做得更大,雙方的效益也就越高。比如寶山鋼鐵公司與上海鋼鐵集團強強聯合也好,最重要的就是將蛋糕做大。在寶鋼與上鋼的強強聯合中,寶鋼有著資金、效益、管理水平、規模等各方面的優勢,上鋼也有著生產技術與經驗的優勢。兩個公司實施強強聯合,充分發揮各方的優勢,發掘更多更大的潛力,形成一個更大更有力的拳頭,將蛋糕做得比原先兩個蛋糕之和還要大。
獵鹿博弈的討論,我們的思路實際只停留在考慮整體效率最高這個角度,而沒有考慮蛋糕做大之後的分配。獵鹿博弈是假設獵人雙方平均分配獵物。
