共找到2條詞條名為開普勒第三定律的結果 展開
- 行星運動三定律之一
- 江映蓉演唱歌曲
開普勒第三定律
行星運動三定律之一
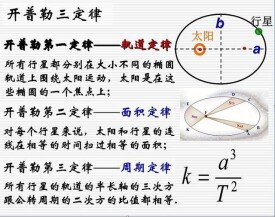
開普勒第三定律也叫行星運動定律。開普勒第三定律的常見表述是:繞以太陽為焦點的橢圓軌道運行的所有行星,其各自橢圓軌道半長軸的立方與周期的平方之比是一個常量。
德國天文學家約翰尼斯·開普勒根據丹麥天文學家第谷·布拉赫等人的觀測資料和星表,通過開普勒本人的觀測和分析后,於1609年在他出版的《新天文學》上發表了關於行星運動的前兩條定律,又於1618年,在《宇宙諧和論》提出了第三條定律。
開普勒第三定律為經典力學的建立、牛頓的萬有引力定律的發現,都作出重要的提示。
開普勒在《宇宙諧和論》上的原始表述:繞以太陽為焦點的橢圓軌道運行的所有行星,其各自橢圓軌道半長軸的立方與周期的平方之比是一個常量。
常見表述:繞同一中心天體的所有行星的軌道的半長軸的三次方(a³)跟它的公轉周期的二次方(T²)的比值都相等,即,(其中M為中心天體質量,k為開普勒常數,這是一個只與被繞星體有關的常量,G為引力常量,其2006年國際推薦數值為G=6.67428×10⁻¹¹N·m²/kg²)不確定度為0.00067×10⁻¹¹m³kg⁻¹s⁻²。
萬有引力定律是用開普勒第三定律導出的,因此不能再用萬有引力定律來推導開普勒第三定律,循環論證是不嚴謹的。開普勒第三定律是開普勒根據第谷的觀測數據來計算出來的,沒有見過推導,推導過程只能是與萬有引力定律的聯繫,不能叫推導。

開普勒的原始數據
開普勒整理數據發現,右圖下方的坐標中各點大致連成一條直線,因此他認為行星的運行周期T和成正比(其中R為軌道半徑),並計算出該直線的斜率為,即 。
方法一:
現實中的星體運動的軌道大多數是橢圓,於是便有以下推導:
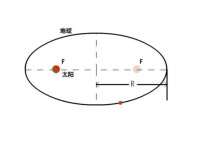
R為半長軸
面積速度為
設各行星繞太陽運行周期為T,橢圓半長軸為a、半短軸為b、太陽到橢圓中心的距離為c
則行星繞太陽運動的周期 。
選近日點A和遠日點B來研究,由ΔS相等可得
從近日點運動到遠日點的過程中,根據機械能守恆定律得:
得 :
由幾何關係得: , ,
所以
整理得。
方法二:
行星繞太陽運動橢圓軌道的面積,根據橢圓的性質則橢圓的面積(a為長軸,b為短軸)由於單位時間內極徑所掃過的面積
則周期 (1)
根據橢圓的性質和開普勒第一定律,半長軸 (2)
(2)式得
(2)式代入(1)式得 (3)
根據橢圓的性質,橢圓的半短軸 ,則 (4)
式(4)代入(3)式得 ,由此式可知繞同一中心天體運行的人造星體軌道半長軸的三次方跟它們的公轉周期的二次方的比值由中心天體的質量所決定。
由運動總能量 ,得 ,則運動周期為
即
其中, , ,和是方程 的根,它們是橢圓運動的兩個轉折點,a為軌道半徑,G為引力常量,M為中心天體的質量。
成立條件
開普勒定律是一個普適定律,適用於一切二體問題。開普勒定律不僅適用於太陽系,他對具有中心天體的引力系統(如行星-衛星系統)和雙星系統都成立。圍繞同一個中心天體運動的幾個天體,它們軌道半徑三次方與周期的平方的比值( )都相等,為 ,M為中心天體質量。這個比值是一個與行星無關的常量,只與中心體質量有關,那麼M相同是這個比值相同。
用開普勒第三定律解決二體問題時,可將兩個質點在相互作用下的運動,可約化為一個質點相對另一個質點的相對運動,質點的質量需改用約化質量,即 ,其中,為兩質點的質量。
拓廣形式
開普勒第三定律也可以表示為:
引入天體質量后可表示為:
其中,為兩個相應的行星質量,,為兩個相應行星圍繞同一恆星運動的周期,, 為兩個行星圍繞同一恆星運動的平均軌道半徑。通過拓展形式,可以根據繞同一行星的兩星體軌道半徑估測星體質量,或根據星體質量估測運行軌道。
實際星體問題大多數為二體問題,實際應用時,人們把開普勒定律看成是牛頓定律和萬有引力定律的表現形式。(M為中心天體質量,m為行星質量)
在 時,可以認為 ,這就是開普勒定律的第三表達式,其中 為開普勒常數。
由此可見,開普勒定律只是一個近似定律。
通過開普勒第三定律,在天體運行中有以下應用:
1.通過測出星體的繞轉周期以及半長軸,算出雙星的質量及估計中心天體的質量;
2.通過兩繞同一中心天體運動的行星的公轉周期,算出這兩行星分別到中心天體的平均距離。(因實際軌道為橢圓形,故採用平均距離)。
3.在星—箭分離問題中,通過星箭橢圓運動周期之比,計算星箭運動軌跡半長軸之比。
二體問題
二體問題是天體力學中的一個基本問題,它是指可視為質點的兩個天體在相互間唯一的萬有引力作用下的運動規律問題。二體問題可以用牛頓萬有引力定律和牛頓運動定律來描述並得到完全解決。開普勒三定律是二體問題的解。
航天
開普勒軌道這個名詞時開普勒以後的人提出來的,並把開普勒軌道擴展到二體問題的解。由於航天器的軌道運動也符合開普勒三定律,因此開普勒軌道同樣適用於航天器。
開普勒軌道的定義:
1.符合開普勒三定律的天體或航天器的運行軌道;
2.由二體問題的解的道德天體或航天器的運行軌道。
由定義可知,開普勒的軌道也稱為二體問題軌道,符合上述定義的開普勒軌道也稱為理想的開普勒軌道。航天器的開普勒軌道可由如下二體問題的基本方程解得:
上述方程描述在慣性坐標系中航天器相對於天體的軌道運動,式中的 是從天體(質量記為)到航天器( )的位置矢量 , 是二體系統的引力常數,G是萬有引力常數。由於,可以只考慮 對 的引力,這種情況可把航天器開普勒軌道看成是限制性二體問題的解,即看成是在慣性固體天體中心引力場中的運動(有心力運動)軌跡。
開普勒第三定律也適用於部分電荷在點電場中運動的情況。因為庫侖力與萬有引力均遵循“平方反比”規律,通過類比可知,帶電粒子在電場中的橢圓運動也遵循開普勒第三定律。
先構造一個勻速圓周運動的模型,根據牛頓第二運動定律和庫侖定律計算圓周運動周期,再將粒子由靜止開始的直線加速運動當做一個無限“扁”的橢圓運動,用開普勒第三定律計算粒子運動時間。

約翰尼斯開普勒
1600年,德國天文學家開普勒應丹麥天文學家第谷之邀,開普勒前往布拉格做第谷的助手。次年,第谷去世,他將自己一生積累的觀測資料留給了開普勒。
開普勒分析第谷測量行星位置的多年記錄(特別是火星的橢圓形軌道),在1619年發表他的第三行星定律。
到了1690年左右,英國人牛頓以“萬有引力”概念解開行星軌道之謎,並且將開普勒第三行星定律改進成,G是萬有引力常數,M是太陽質量,m是行星質量,P是公轉周期。
19世紀初德國數學家高斯將牛頓的式子改寫為 ,其中k為高斯引力常數, 成為了G的“代用品”。
到了19世紀後期,物理量(包括G、M、m、a和光速c)較前代測得更準確,當時的美國海軍天文台台長紐康負責編算天文年曆,他把高斯引力常數k值修訂。1976年,1A.U.採用紐康的k值和開普勒第三定律來釐定天文單位的定義
1798年,英國科學家亨利·卡文迪許通過扭秤實驗,測量出中了引力常量G的大小是G=6.754×10⁻¹¹N·m²/kg²,卡文迪許對G的測量進一步完善了開普勒第三定律。G在2006年的國際推薦值為G=6.67428×10⁻¹¹N·m²/kg²。
開普勒的定律給予亞里士多德派與托勒密派在天文學與物理學上極大的挑戰。他的論點,打破了亞里士多德留下的天文學與物理學中的陳舊觀念。
開普勒定律的一個重要功績,就是後來在1684年牛頓根據開普勒定律及自己研究的運動定律,破譯了天文運動的機密——萬有引力定律。
開普勒的三定律是天文學的一次革命,它摧毀了托勒密繁雜的本輪宇宙體系,完善和簡化了哥白尼的日心宇宙體系。它對後人尋找出太陽繫結構的奧秘具有重大的啟發意義,為經典力學的建立、牛頓的萬有引力定律的發現,都作出重要的提示。