輻角
輻角
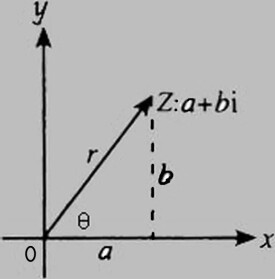
輻角,複數的模與輻角是複數三角形式表示的兩個基本元素,複數所對應的向量長度稱為複數的幅值,該向量與實軸正方向的夾角為複數的輻角。輻角的大小有無窮多,但是輻角主值唯一確定。利用複數的模和輻角,可以將複數表示成三角表示式和指數表示式,並可以和代數表示式之間互相轉化,以方便討論不同問題時的需要。
由直角坐標與極坐標的關係可知,非零有窮複數可以用其模與輻角來表示,即得利用歐拉公式。
分別稱第一式和第三式為非零複數的三角表示式和指數表示式,這三種表示式可以和代數表示式之間互相轉化,以方便討論不同問題時的需要。
一個非零複數的輻角有無窮多個值,它們相差的整數倍,但中只有一個值滿足條件,稱為複數的主輻角。
當時的輻角沒有意義。
複數的主輔角與反正切的主值有以下關係:

輻角
輻角
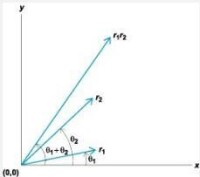
為該複數的三角式;
為該複數的指數式。
其中ρ為該複數的模,φ稱為該複數中的輻角,記作Arg z。一個複數的輻角值不能唯一地確定,可以取無窮多個值,並且彼此相差2π的整數倍。通常約定argz滿足條件的一個特定的值,並稱argz為Argz的主值,或z的主輻角。>
大學基礎物理中在光學和電磁學會涉及到輻角的知識。