地圖投影
地圖投影
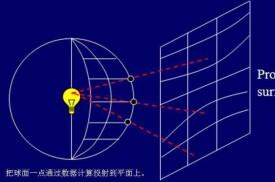
地圖投影是利用一定數學法則把地球表面的經、緯線轉換到平面上的理論和方法。
地圖投影
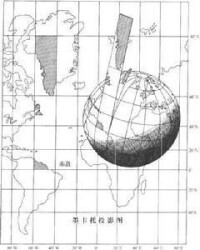
由於球面上任何一點的位置是用地理坐標(λ,φ)表示的,而平面上的點的位置是用直角坐標(χ,у)或極坐標(r,)表示的,所以要想將地球表面上的點轉移到平面上,必須採用一定的方法來確定地理坐標與平面直角坐標或極坐標之間的關係。這種在球面和平面之間建立點與點之間函數關係的數學方法,就是地圖投影方法。地圖投影變形是球面轉化成平面的必然結果,沒有變形的投影是不存在的。對某一地圖投影來講,不存在這種變形,就必然存在另一種或兩種變形。但製圖時可做到:在有些投影圖上沒有角度或面積變形;在有些投影圖上沿某一方向無長度變形。
地球橢球體表面是個曲面,而地圖通常是二維平面,因此在地圖製圖時首先要考慮把曲面轉化成平面。然而,從幾何意義上來說,球面是不可展平的曲面。要把它展成平面,勢必會產生破裂與褶皺。這種不連續的、破裂的平面是不適合製作地圖的,所以必須採用特殊的方法來實現球面到平面的轉化。

地球
根據地圖投影的一般公式,只要知道地面點的經緯度(λ,φ),便可以在投影平面上找到相對應的平面位置(χ,у),這樣就可按一定的製圖需要,將一定間隔的經緯網交點的平面直角坐標計算出來,並展繪成經緯網,構成地圖的“骨架”。經緯網是製作地圖的“基礎”,是地圖的主要數學要素。
地圖投影
幾何透視法
最早使用投影法繪製地圖的是公元前3世紀古希臘地理學家埃拉托色尼。在這之前地圖投影曾用來編製天體圖(不過天體圖的投影是從天球投影到平面,而不是地球;但兩者原理相同)。埃拉托色尼在編製以地中海為中心的當時已知世界地圖時,應用了經緯線互相垂直的等距離圓柱投影。1569年,比利時的地圖學家墨卡托首次採用正軸等角圓柱投影編製航海圖,使航海者可以不轉換羅盤方向,而採用大圓直線導航。卡西尼父子設計的用於三角測量的投影及蘭勃特提出的等角投影理論和設計出的等角圓錐、等面積方位和等面積圓柱投影,使得17-18世紀的地圖投影具有了時代的特點。19世紀,地圖投影主要保證大比例尺地圖的數學基礎,以適應軍事製圖發展和地形測量擴大的需要。19世紀還出現了高斯投影,它是德國高斯設計提出的橫軸等角橢圓柱投影,這種投影法經德國克呂格爾加以補充,成為高斯-克呂格爾投影。19世紀末期以後俄國一些學者對投影作了較深入地研究,對圓錐投影常數的確定提出了新見解,又提出了根據已知變形分佈推求新投影和利用數值法求出投影坐標的新方法。20世紀50年代以來中國提出了雙重方位投影、雙標準經線等角圓柱投影等新方法。20世紀60年代以來,美國學者對地圖投影的研究結果,提出空間投影、變比例尺地圖投影和多交點地圖投影,為人造地球衛星等提供了所需的投影。
1、按變形方式
(1)等角投影,又稱正形投影,指投影面上任意兩方向的夾角與地面上對應的角度相等。在微小的範圍內,可以保持圖上的圖形與實地相似;不能保持其對應的面積成恆定的比例;圖上任意點的各個方向上的局部比例尺都應該相等;不同地點的局部比例尺,是隨著經、緯度的變動而改變的。
(2)等(面)積投影,地圖上任何圖形面積經主比例尺放大以後與實地上相應圖形面積保持大小不變的一種投影方法。等積投影相反,保持等積就不能同時保持等角。
(3)任意投影。任意投影為既不等角也不等積的投影,其中還有一類“等距(離)投影”,在標準經緯線上無長度變形,多用於中小學教學圖。
2、根據正軸投影時經緯網的形狀分類
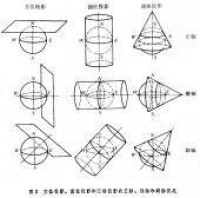
a>幾何投影(利用透視的關係,將地球體面上的經緯網投影到平面上或可展位平面的圓柱面和圓錐面等幾何面上。)分以下三種:
(1)平面投影(plane projection) ,又稱方位投影,將地球表面上的經、緯線投影到與球面相切或相割的平面上去的投影方法;平面投影大都是透視投影,即以某一點為視點,將球面上的圖象直接投影到投影面上去。
(2)圓錐投影(conical projection),用一個圓錐面相切或相割於地面的緯度圈,圓錐軸與地軸重合,然後以球心為視點,將地面上的經、緯線投影到圓錐面上,再沿圓錐母線切開展成平面。性質:地圖上緯線為同心圓弧,經線為相交於地極的直線。
(3)圓柱投影(cylindrical projection),用一圓柱筒套在地球上,圓柱軸通過球心,並與地球表面相切或相割將地面上的經線、緯線均勻的投影到圓柱筒上,然後沿著圓柱母線切開展平,即成為圓柱投影圖網。
(4)多圓錐投影:投影中緯線為同軸圓圓弧,而經線為對稱中央直徑線的曲線。
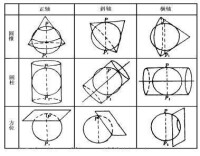
投影分類
(2)偽圓柱投影,在圓柱投影基礎上,規定緯線仍為同心圓弧,除中央經線仍為直線外,其餘經線則投影成對稱於中央經線的曲線。
(3)偽圓錐投影,投影中緯線為同心圓圓弧,經線為交於圓心的曲線。
3、根據投影面與地球表面的相關位置分類(投影軸與地軸的關係)
(1)正軸投影(重合):投影面的中心線與地軸一致
(2)斜軸投影(斜交):投影面的中心線與地軸斜交
(3)橫軸投影(垂直):投影面的中心線與地軸垂直
4、幾何投影中根據投影面與地球表面的關係
(1)切投影
(2)割投影
5、投影的應用
(1)圓錐投影:主要應用於中緯度地區沿著東西伸展區域的國家地區。
(2)圓柱投影:是圓錐投影的一個特殊情況,正軸圓柱投影表現為相互正交的直線。等角圓柱投影(墨卡托)具有等角航線表現為直線的特性,因此最適宜編製各種航海、航空圖。
(3)方位投影:等變形線為同心圓,最適宜表示圓形輪廓的區域,如表示兩極地區的地圖。
常用的投影方法 有墨卡托投影(正軸等角圓柱投影)、高斯-克呂格投影、斜軸等面積方位投影、雙標準緯線等角圓錐投影、等差分緯線多圓錐投影、正軸方位投影等。
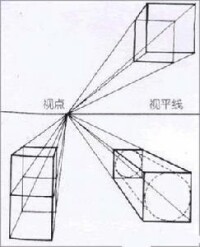
幾何透視法是利用透視的關係,將地球體面上的點投影到投影面(藉助的幾何面)上的一種投影方法。如假設地球按比例縮小成一個透明的地球儀般的球體,在其球心或球面、球外安置一個光源,將球面上的經緯線投影到球外的一個投影平面上,即將球面經緯線轉換成了平面上的經緯線。幾何透視法是一種比較原始的投影方法,有很大的局限性,難於糾正投影變形,精度較低。絕大多數地圖投影都採用數學解析法。
數學解析法是在球面與投影面之間建立點與點的函數關係,通過數學的方法確定經緯線交點位置的一種投影方法。大多數的數學解析法往往是在透視投影的基礎上,發展建立球面與投影面之間點與點的函數關係的,因此兩種投影方法有一定聯繫。
地圖投影的建立系假定有一個投影面(平面、可展的圓錐面或圓柱面)與投影原面(地球橢球面)相切、相割或多面相切,如圖1
所示。用某種投影條件將投影原面上的地理坐標點一一投影到平面坐標系內,即構成某種地圖投影。其實質是將地球橢球面上地理坐標(φ、λ)轉化為平面直角坐標(x、y)。它們之間的數學關係式為:
x=f1(φ、λ);y=f2(φ、λ)
式中f1、f2為函數。
地圖投影
正軸割圓錐等面積投影(等積圓錐投影)
投影參數:
起算緯度:0°或10°N
中央經線:105°E 或110°E
標準緯線1:25°N
標準緯線2:45°N 或47°N
採用原因:
1、中國大部分地方屬於中低緯度地區,故採用圓錐投影。
2、中國疆域遼闊,緯度跨度很大(有50°的緯差),故必須用割投影(雙標準緯線)來控制形變。
3、為強調各省區之間和中國與相鄰國家之間的面積對比關係,採用等面積投影。
製圖的區域的位置、形狀和範圍,地圖的比例尺、內容、出版方式影響了投影的種類。比如在極地就應該是正軸方位投影,中緯地區使用正軸圓錐投影。
製作地形圖通常使用高斯-克呂格投影,製作區域圖通常使用方位投影、圓錐投影、偽圓錐投影,製作世界地圖通常使用多圓錐投影、圓柱投影和偽圓柱投影。但通常而言,要依據實際情況具體選擇。