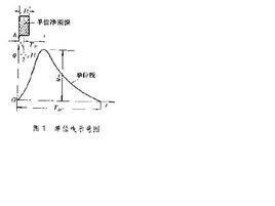
單位過程線

單位時間內流域上均勻分佈的單位凈雨量在流域出口斷面處形成的地面徑流量過程線。簡稱單位線。單位凈雨量通常取雨深10毫米；單位歷時可以是一個時段如1小時、3小時、6小時等，也可以是瞬時，即凈雨歷時趨於無限小的情況。相應於前者的單位線稱為時段單位線，相應於後者的稱為瞬時單位線。單位線是按某些基本假定，利用流域的實際降雨和與其相應的出口斷面處的流量過程資料分析得出的。它是應用水文學中最基本的分析工具之一，主要用於由暴雨過程推求流量過程，在水文分析計算和水文預報中廣泛應用。

在近代匯流理論中，把流域降雨徑流的匯流現象看作一個線性系統，降雨作為系統的輸入，徑流量過程作為系統的輸出，而流域的單位線就是這個線性系統的響應函數。它應滿足下列假定：①倍比假定。即單位時段內凈雨深若不是一個單位而是 n 個單位，則它所形成的流量的過程線的底長與單位線底長相同，地面流量過程線的縱標為單位線縱標的 n 倍;②疊加假定。降雨歷時如果不是一個時段而是 m 個時段，則各時段凈雨所形成的流量過程彼此獨立互不影響，出口斷面處的流量是這 m 個流量過程之和。正確判斷上述假定與實際情況的差異，特別是降雨特性對單位線的影響，是正確應用單位線這一工具的中心課題。

1932年由美國L.R.K.謝爾曼提出。時段單位線最好用降雨時空分佈比較均勻，凈雨歷時較短，降雨強度較大的單獨洪水資料推求。若凈雨歷時只有一個時段，而且分佈均勻，可直接將地面徑流過程線縱坐標除以凈雨量的單位數 n，即得單位線。如凈雨時段有兩個或兩個以上，可根據單位線假定，用分析法或試演演算法求得。

不同時段單位線可以利用 S- 曲線相互轉換，時段單位線的 S-曲線是指將同一單位線沿時間坐標每隔一單位時段錯開，然後將同一時刻的縱坐標累加而求得的一條累積流量和時間的關係曲線。若將時段為 T1 的單位線轉化成時段為 T2 的單位線，只需把相應於 T1 時段單位線的 S-曲線沿時間坐標后移 T2小時，並將相同時刻縱坐標之差值乘

，即得 T2時段單位線。

20世紀30年代，美國土木工程師學會的報告中已出現了“瞬時降雨的出流過程線可作為流域特性的代表”的概念。1945年，美國人C.O.克拉克把這一概念用於單位線的推求中，提出了“瞬時單位線”一詞，但他未得到瞬時單位線的數學表達式，而是將面積-流時曲線經過一次調蓄演算後作為瞬時單位線。50年代後期，許多水文學家從事瞬時單位線的研究，愛爾蘭人J.E.納什於1957、1960年給出了瞬時單位線的數學表達式並逐漸形成了一個較完整的體系，納什把流域作為一連串調蓄作用相同、彼此串連的水庫群，並假定每個水庫的蓄泄關係是線性的。這樣，凈雨在流域上的匯流過程便可模擬為流量自進入最上一個水庫后，通過 n個串連水庫直至從最末一個水庫流出的一連串調蓄過程，從而導出瞬時單位線的方程為：

式中 n、 K為反映流域調蓄特性的參數；Γ 為伽瑪函數；e為自然對數的底； t為時間變數； U(0， t)為 t時刻瞬時單位線的縱坐標。瞬時單位線形狀取決於參數 n 和 K。不同流域的 n 和 K 不同，瞬時單位線形狀也不同，一旦確定了某流域的 n 和 K,該流域的瞬時單位線也便惟一地確定了。 n、 K可通過計算凈雨過程和實測的流量過程的一階原點矩和二階中心矩求出或採用優選法求出。

瞬時單位線的主要優點在於，它不受凈雨歷時的影響，有一定數學表達式，便於進行數學處理和區域綜合。在實際應用時需首先將瞬時單位線轉換為時段單位線。對上式進行積分，可得瞬時單位線的 S-曲線方程：

將 S( t)曲線移后Δ t小時得 S( t-Δ t)曲線，兩條曲線縱坐標之差【 S( t)- S( t-Δ t)】乘以因次轉換係數，即得時段為Δ t的時段單位線。 S( t)曲線已製成表格可備查用。

指根據流域特徵與單位線要素或參數之間的經驗關係，由流域特徵推求出單位線要素而求得的單位線。流域自然地理特徵一般指流域面積 F，平均比降 J 等；單位線要素一般指時段單位線的洪峰流量 qm，洪峰滯時 tp，單位線底長 T,或瞬時單位線參數 m1(= n. K)等。1938年F.F.斯奈德提出了綜合單位線。

一般先進行單位線的單站綜合，然後進行單位線的地區綜合，供推求無資料地區單位線應用。①單位線的單站綜合。對一特定流域，由各次降雨和流量資料分析得來的單位線，若差別不大，可取其平均值作為該流域的單位線。然而，降雨特性(強度和暴雨中心位置等)往往對單位線有明顯影響，這時可建立經驗關係，如時段單位線洪峰流量 qm或滯時 tp與時段凈雨深 h的經驗關係，或建立瞬時單位線參數 m1與時段Δ t內凈雨強度i(= h/Δ t)的關係：

式中 c1、 c2、 c3和 ɑ1、 ɑ2、 ɑ3為經驗係數和指數。②單位線的地區綜合。時段單位線一般只對洪峰進行地區綜合，其他要素可間接確定：

瞬時單位線一般只對參數 m1進行綜合， m2採用地區平均值：

c4、 c5， ɑ7、 ɑ5，i7、i5分別為經驗係數和指數。

在廣泛使用單位線的實踐過程中，人們早就發現單位線的線性理論和實際雨洪匯流現象並不相符。1935年R.E.霍頓提出地表徑流的漲洪段依賴於有效降雨強度，揭示了流域匯流非線性現象；1960年N.E.明歇爾發表了他的試驗資料分析成果，第一次明確提出了雨強和單位線之間存在著非線性關係，即雨強愈大單位線峰值愈高，形狀尖瘦；而雨強愈小，峰值愈低，形狀矮胖。引起單位線變化的因素主要是凈雨在流域上分佈的不均勻性及凈雨強度的變化。這些因素使得各次洪水在匯流過程中，因匯流速度及流域調蓄作用的變化而破壞了單位線的線性假定。由於單位線是一個經驗的方法，處理非線性變化只能作出經驗改正。為了處理凈雨在流域上分佈的不均勻性，常把單位線應用於較小流域，一般不宜超過1000平方公里。對於凈雨強度的變化，可作出雨強對單位線的非線性改正。50年代初期，中國在治淮工作中用單位線計算水庫工程的設計洪水時，治淮工程指揮部工程部第一次提出單位線要素峰量的非線性改正。1977年水電部洪水預報會戰小組，分析了海河、淮河流域發生的特大洪水資料，提出了小流域單位線的非線性規律和變雨強單位線分析方法。

R.K.林斯雷等著，劉光文等譯：《工程水文學》，水利出版社，北京，1981。(R.K.Linsley，Jr.，et al.，Hydrology for Engineers,2nd ed.，McGraw-Hill,New York，1975.) 陳家琦、張恭肅著：《小流域暴雨洪水計算》，水利電力出版社，北京，1985。