離群點
離群點
離群點是指一個時間序列中,遠離序列的一般水平的極端大值和極端小值。
離群點,因此,也稱之為歧異值,有時也稱其為野值。
概括的說,離群點是由於系統受外部干擾而造成的。但是,形成離群點的系統外部干擾是多種多樣的。首先可能是採樣中的誤差,如記錄的偏誤,工作人員出現筆誤,計算錯誤等,都有可能產生極端大值或者極端小值。其次可能是被研究現象本身由於受各種偶然非正常的因素影響而引起的,例如。在人口死亡序列中,由於某年發生了地震,使該年度死亡人數劇增,形成離群點;在股票價格序列中,由於受某項政策出台或某種謠傳的刺激,都會出現極增,極減現象,變現為序列中的離群點。
不論是何種原因引起的離群點對以後的時間序列分析都會造成一定的影響。從造成分析的困難來看,統計分析人員說不希望序列中出現離群點,離群點會直接影響模型的擬合精度,甚至會得到一些虛偽的信息。例如,兩個相距很近的離群點將在譜分析中產生許多虛假的頻率。因此,離群點往往被分析人員看作是一個“壞值”。但是,從獲得信息來看,離群點提供了很重要的信息,它不僅提示我們認真檢查採樣中是否存在差錯,在進行時間序列分析前,認真確認序列,而且,當確認離群點是由於系統受外部突發因素刺激而引起的時候,他會提供相關的系統穩定性,靈敏性等重要信息。
在時間序列分析中通常把離群點分為四種類型進行處理。第一類是加性離群點。造成這種離群點的干擾,隻影響該干擾發生的那一時刻T上的序列值,即XT而不影響該時刻以後的序列值;第二種是更新離群點,造成離群點的干擾不僅作用於XT,而且影響T時刻以後序列的所有觀察值,它的出現意味著一個外部干擾作用於系統的開始,並且其作用方式與系統的動態模型有關;第三種樹水平位移離群點,造成這種離群點的干擾素在某一時刻T,系統的結構發生了變化,並持續影響T時刻以後的所有行為,在數列上往往變現為T時刻前後的序列均值發生水平位移;第四種是暫時變更離群點,造成這種離群點的干擾是在T時刻干擾發生時具有一定初始效應,以後隨時間根據衰減因子的大小呈指數衰減的一類干擾事件。
總結一下,離群點(outlier)是一個數據對象,它顯著不同於其他數據對象,就像是被不同的機制產生一樣,在樣本空間中,與其他樣本點的一般行為或特徵不一致的點。值得注意的是,離群點並不是異常值。(比如說,A月薪50w,B、C、D月薪5000,雖然A月薪異常於樣本集,是離群點,但是它並不是異常值。)
離群點檢驗就是通過多種檢測方法找出其行為不同於預期對象的數據點的過程。
根據正常數據和離群點的假定分類,可以分為以下4種方法:
離群點概率定義:離群點是少數異常於正常數據集的數據對象,在概率分佈模型中,具有低概率。
基於統計的離群點檢測一般遵循以下思路:
設定數據集的分佈模型——不和諧檢驗——發現離群點
因為離群點在概率分佈模型中低概率出現,可以通過檢測低概率的數據對象或數據樣本,不過缺點也較為明顯,低概率出現的樣本不一定也是離群點(比如進貨客戶群中,進貨量大的客戶雖然少,但是也是我們需要的對象)
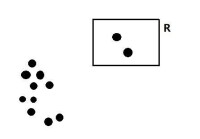
離群點
比如說,使用數據對象的三個最近鄰來進行建模,那麼R區域裡面的顯著不同於該數據集的其他對象點;對應R中的對象,它們的第二個第三個最近鄰都顯著比其他對象的更遠(超出一定的標差),因此可以將R區域中的對象作一個標記為基於鄰近性的離群點。
通過考察對象與簇之間的關係檢測離群點,換而言之,離群點是一個對象,它屬於小的稀疏簇或者不屬於任何簇。
主要有幾種考察方法:
該對象屬於某個簇嗎?如果不屬於,則被識別為離群點;(比如群居動物,山羊兔子成群居住和遷移,那麼這些數據對象會劃分為一個簇,這樣可以不屬於這些簇的數據對象識別為離群點)
該對象與最近的簇之間的距離很遠嗎?如果遠,則被識別為離群點;
該對象是小簇或稀疏簇的一部分嗎?如果是,則該簇內所有對象被識別為離群點;
如果訓練數據中有類標號,則可以將其視為分類問題,該問題思路一般是:訓練一個可以區分“正常數據”和離群點的分類模型。(一個人到銀行是否辦理貸款業務,辦理與不辦理就是2個類標號)
通常使用一類模型(one-class model),也就是構造一個僅僅描述正常類的分類器,這樣不屬於正常類的樣本就是離群點,僅使用正常類檢測離群點可以檢測不靠近訓練集中的離群點的新離群點;這樣,當一個新離群點進來時,只要它位於正常類的決策邊界內就為正常點,在決策邊界外就為離群點。(決策邊界的構建可以參考SVM:支持向量機)
正常數據與異常數據之間的邊界通常並不清晰,它們之間通常有很寬的灰色地帶。通常為正常點構建一個綜合模型有一定挑戰性的,那麼對離群點檢測便更是具有挑戰性。
通常,我們通過相似性或者距離度量來描述數據對象之間的聯繫,但是往往度量的選擇依賴於應用。例如,在醫療分析、欺詐檢測中,小偏離就可能是重要的,足以證實離群點。相反,在市場分析中,對象通常波動很大,顯著的偏差才能證實離群點。所以離群點的檢測高度依賴於應用類型使得我們不可能開發通用的離群點檢測方法。
離群點不同於雜訊,實際數據質量往往很差。低質量的數據和雜訊給離群點檢測帶來了巨大的挑戰。它們可能扭曲數據,模糊正常對象與離群點之間的差別;此外,雜訊和缺失數據可能“掩蓋”離群點,降低離群點檢測的有效性。(噪音數據指出現在某變數上的隨機誤差或變異)
用戶不僅要檢測離群點,而且要知道被檢測到的點為什麼是離群點。為了滿足可理解性要求,離群點檢測方法必須提供某種檢測理由。