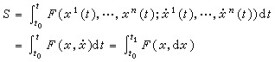一般空間微分幾何學

20世紀以來，因受到廣義相對論的影響，黎曼幾何發展很快，從此產生了以更一般的曲線長度積分為基礎的芬斯勒空間，以超曲面的面積積分為基礎的嘉當空間，以二階微分方程組為基礎的道路空間和K展空間等等，而這些通稱一般空間。

芬斯勒空間 設M是參考於一系坐標xi(i=1,2,…,n)的n維集合，並且它的曲線xi=xi(t)的“弧長”是按照積分

定義起來的（其中，ρ>0)。這時，稱M為芬斯勒空間。特別是，當

時，得到黎曼空間。P.芬斯勒(1918)在其學位論文中曾經把黎曼空間的一些結果拓廣到這個空間來，但是它的微分幾何到É.嘉當(1934)才逐漸趨於完整。例如，這個空間仿射聯絡的確定，曲率論的建立等研究，都是以後才發展起來的。僅僅要指出，芬斯勒空間的測地線（即上列積分的極值曲線）的微分方程具有如下的形式：

式中是由F(x,凧)確定的某種函數組。

近年來，無限維的芬斯勒流形在非線性分析中有重要作用。

嘉當空間 在n維空間里，以(n-1)維超曲面領域的表面積概念為基礎而構成的幾何，稱n維嘉當空間幾何。設(x)=( x1,x2,…，xn)表示空間一點的坐標,(u)=(u1,u2,…，un)表示該點切空間的(n-1)維子空間的齊次坐標，(x，u)稱為點(x)的超平面素。以B表示超平面素所成的一個區域，採用一個在B是正則的而且取正值的函數L（x,u），這裡L關於ui是正齊一次的，L(x,ρu)=ρL(x,u)，(ρ>0)，並約定，在超平面素(x,u)的(n-1)維表面積元素為

為了改寫dO,設是光滑超曲面F的正則參數表示。從(n-1)×n矩陣刪去第k行，而且用(-1)k+1pk表示這樣得出的(n-1)階行列式。那麼，從上列的約定便導出一個在有向超曲面F的區域上的(n-1)重積分

它表示了這個區域的“(n-1)維表面積”。

從基本函數 L（x，u）作 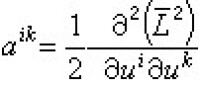且令α＝det|αik|，嘉當的測度張量可表成

這樣，這種空間微分幾何便有了發展的基礎，特別重要的是研究面積積分的第一和第二變分，以及極值離差理論，即能保持極值超曲面的無窮小變形的方程。

K展空間 設在N 維空間SN里給定了一組K 維流形，使得組中有一個且僅有一個流形通過一般位置下的任何K+1個鄰近點，或者和任何一個已知的K維元素（按照一點和其銜接的K維平坦流形組成的元素）相切。這些K維流形簡稱K展，具有這種結構的N維空間SN稱K展空間。特別是，當K=1時，SN就是道路空間。

設(xi;i=1,2,…,N)是SN的一點的坐標，那麼每個K展可表成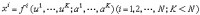或簡寫為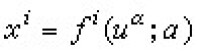,式中各函數是變數u和參數α的解析函數（或充分光滑的函數）。從定義易知

如果由K展的表達式消去參數α,便獲得仿射K展空間的偏微分方程組

式中函數是p的齊二次函數。

根據J.道格拉斯導進一個仿射聯絡到仿射 K展空間SN：

從而把上列偏微分方程組改寫成

。

從這個仿射聯絡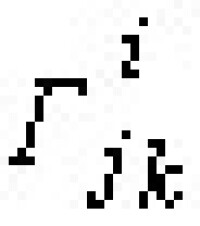不但可以導出仿射曲率張量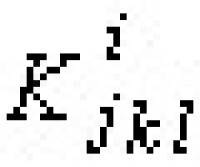,還可作出射影聯絡以及有關的偏微分方程組的可積分條件，還可證明；嘉當的“平面公理”的成立與空間為射影平坦是等價的。

蘇步青著：《一般空間的微分幾何學》，科學出版社，北京，1958。