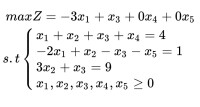大M法
數學中的解題方法
大M法(big M method)是線性規劃問題的約束條件(=)等式或(≥)大於型時,使用人工變數法后,尋找其初始基可行解的一種方法。
在線性規劃問題的約束條件中加人工變數后,要求在目標函數中相應地添加認為的M或一M為係數的項。在極大化問題中,對人工變數賦於一M作為其係數;在極小化問題中,對人工變數賦於一個M作為其係數,M為一任意大(而非無窮大)的正數。把M看作一個代數符號參與運算,用單純形法求解,故稱此方法為大M法。
應用單純形法在改進目標函數的過程中,如果原問題存在最優解,必然使人工變數逐步變為非基變數,或使其值為零。否則,目標函數值將不可能達到最小或最大。在迭代過程中,若全部人工變數變成非基變數,則可把人工變數所在的列從單純形表中刪去,此時便找到原問題的一個初始基可行解。若此基可行解不是原問題的最優解,則繼續迭代,直至所有的檢驗數都小於等於0,求得最優解為止。
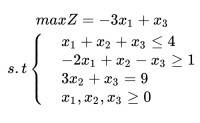
大M法

大M法
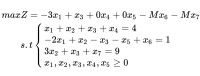
大M法
| C→(目標函數係數) | -3 | 1 | -M | -M | |||||
| C | 基 | b | x | x | x | x | x | x | x |
| x | 4 | 1 | 1 | 1 | 1 | ||||
| -M | x | 1 | -2 | [1] | -1 | -1 | 1 | ||
| -M | x | 9 | 3 | 1 | |||||
| c-z | -2M-3 | 4M | 1 | -M | |||||
| x | 3 | 3 | 2 | 1 | 1 | -1 | |||
| x | 1 | -2 | 1 | -1 | -1 | 1 | |||
| -M | x | 6 | [6] | 4 | 3 | -3 | 1 | ||
| c-z | 6M-3 | 4M+1 | 3M | -4M | |||||
| x | 1 | -1/2 | -1/2 | -1/2 | |||||
| x | 3 | 1 | 1/3 | 1/3 | |||||
| -3 | x | 1 | 1 | 2/3 | 1/2 | -1/2 | 1/6 | ||
| c-z | 3 | 3/2 | -M-3/2 | -M+1/2 | |||||
| x | 1 | -1/2 | 1/2 | -1/2 | |||||
| x | 5/2 | -1/2 | 1 | -1/4 | 1/4 | 1/4 | |||
| 1 | x | 3/2 | 3/2 | 1 | 3/4 | -3/4 | 1/4 | ||
| c-z | -9/2 | -3/4 | -M+3/4 | -M-1/4 | |||||
關於大M法的單純形表可以和兩階段法進行對比參照,可以發現二者很大程度上是相同的。

合併圖冊