共找到2條詞條名為偽隨機數的結果 展開
- 偽隨機數
- 種子數
偽隨機數
偽隨機數
偽隨機數是用確定性的演演算法計算出來自[0,1]均勻分佈的隨機數序列。並不真正的隨機,但具有類似於隨機數的統計特徵,如均勻性、獨立性等。在計算偽隨機數時,若使用的初值(種子)不變,那麼偽隨機數的數序也不變。偽隨機數可以用計算機大量生成,在模擬研究中為了提高模擬效率,一般採用偽隨機數代替真正的隨機數。模擬中使用的一般是循環周期極長並能通過隨機數檢驗的偽隨機數,以保證計算結果的隨機性。
一般地,偽隨機數的生成方法主要有以下3種:
(1)直接法(Direct Method),根據分佈函數的物理意義生成。缺點是僅適用於某些具有特殊分佈的隨機數,如二項式分佈、泊松分佈。
(2)逆轉法(Inversion Method),假設U服從[0,1]區間上的均勻分佈,令X=F-1(U),則X的累計分佈函數(CDF)為F。該方法原理簡單、編程方便、適用性廣。
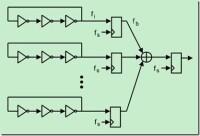
偽隨機數發生器
因此,偽隨機數生成器(PRNG)一般採用逆轉法,其基礎是均勻分佈,均勻分佈PRNG的優劣決定了整個隨機數體系的優劣[7]。下文研究均勻分佈的PRNG。
C語言程序例
偽隨機數
這個程序(rand01.c)完整地闡述了隨機數產生的過程:
首先,主程序調用random_start()方法,random_start()方法中的這一句我很感興趣:
movedata(0x0040,0x006c,FP_SEG(temp),FP_OFF(temp),4);

偽隨機數理論推導
random用來根據隨機種子RAND_SEED的值計算得出隨機數,其中這一句:
RAND_SEED=(RAND_SEED*123+59)%65536;
是用來計算隨機數的方法,隨機數的計算方法在不同的計算機中是不同的,即使在相同的計算機中安裝的不同的操作系統中也是不同的。我在linux和windows下分別試過,相同的隨機種子在這兩種操作系統中生成的隨機數是不同的,這說明它們的計算方法不同。
現在,我們明白隨機種子是從哪兒獲得的,而且知道隨機數是怎樣通過隨機種子計算出來的了。那麼,隨機種子為什麼要在內存的0040:006CH處取?0040:006CH處存放的是什麼?
學過《計算機組成原理與介面技術》這門課的人可能會記得在編製ROM BIOS時鐘中斷服務程序時會用到Intel 8253定時/計數器,它與Intel 8259中斷晶元的通信使得中斷服務程序得以運轉,主板每秒產生的18.2次中斷正是處理器根據定時/記數器值控制中斷晶元產生的。在我們計算機的主機板上都會有這樣一個定時/記數器用來計算當前系統時間,每過一個時鐘信號周期都會使記數器加一,而這個記數器的值存放在哪兒呢?沒錯,就在內存的0040:006CH處,其實這一段內存空間是這樣定義的:
TIMER_LOW DW ? ;地址為 0040:006CH
TIMER_HIGH DW ? ;地址為 0040:006EH
TIMER_OFT DB ? ;地址為 0040:0070H
時鐘中斷服務程序中,每當TIMER_LOW轉滿時,此時,記數器也會轉滿,記數器的值歸零,即TIMER_LOW處的16位二進位歸零,而TIMER_HIGH加一。rand01.c中的
movedata(0x0040,0x006c,FP_SEG(temp),FP_OFF(temp),4);
正是把TIMER_LOW和TIMER_HIGH兩個16位二進位數放進temp數組,再送往RAND_SEED,從而獲得了“隨機種子”。
現在,可以確定的一點是,隨機種子來自系統時鐘,確切地說,是來自計算機主板上的定時/計數器在內存中的記數值。這樣,我們總結一下前面的分析,並討論一下這些結論在程序中的應用:
1.隨機數是由隨機種子根據一定的計算方法計算出來的數值。所以,只要計算方法一定,隨機種子一定,那麼產生的隨機數就不會變。
C++程序例

偽隨機數理論推導
在相同的平台環境下,編譯生成exe后,每次運行它,顯示的隨機數都是一樣的。這是因為在相同的編譯平台環境下,由隨機種子生成隨機數的計算方法都是一樣的,再加上隨機種子一樣,所以產生的隨機數就是一樣的。
2.只要用戶或第三方不設置隨機種子,那麼在默認情況下隨機種子來自系統時鐘(即定時/計數器的值)
C++程序例2
看下面這個C++程序:
這裡用戶和其他程序沒有設定隨機種子,則使用系統定時/計數器的值做為隨機種子,所以,在相同的平台環境下,編譯生成exe后,每次運行它,顯示的隨機數會是偽隨機數,即每次運行顯示的結果會有不同。
3.建議:如果想在一個程序中生成隨機數序列,需要至多在生成隨機數之前設置一次隨機種子。
生成一個隨機字元串
看下面這個用來生成一個隨機字元串的C++程序: (原來的程序我編譯不了,就改了改,加了一些頭文件)(我不是上面那個括弧里的人。我又對源程序進行了一下簡化,可以實現相同的功能)
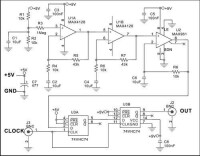
偽隨機數發生器
總結
1.計算機的偽隨機數是由隨機種子根據一定的計算方法計算出來的數值。所以,只要計算方法一定,隨機種子一定,那麼產生的隨機數就是固定的。
2.只要用戶或第三方不設置隨機種子,那麼在默認情況下隨機種子來自系統時鐘。
① 0假設(null hypothesis)為樣本服從均勻分佈;② 1假設(alternative hypothesis)為樣本不服從均勻分佈。
採用P值(∈[0, 1])衡量,P值越趨近於0,表示越有理由拒絕0假設,即樣本不服從均勻分佈;P值越趨近於1,表示越有理由接受0假設,即樣本服從均勻分佈。
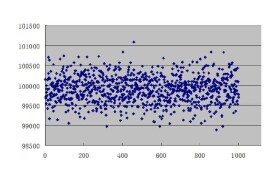
如圖1與圖2所示:隨著P值下降,樣本也越來越不服從均勻分佈。實踐中希望P值越大越好。然而統計學的結論顯示,P值一定服從均勻分佈,與N、S大小無關,這表明由於隨機性,總會出現某次抽樣得到的樣本不服從、甚至遠離均勻分佈。另外,樣本大小的不同,造成檢驗標準的不同,直觀上看S=100對應的均勻分佈普遍比S=20對應的更均勻。因此,小樣本情況下均勻分佈PRNG的差異性尤為嚴重。