漢德公式
漢德公式
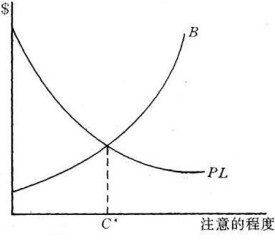
在美利堅合眾國政府訴卡羅爾拖輪公司一案中,法官漢德(Learned Hand)提出了著名的漢德公式:B
漢德公式(The Hand Formula)由美國聯邦上訴法院第二巡迴庭著名法官勒·漢德在1942年美利堅合眾國訴卡洛爾拖船公司(以下簡稱卡洛爾案)一案中正式提出,因此有時也被稱作卡洛爾學說或卡洛爾公式(The Carroll Towing Doctrine or Carroll Towing Formula)。卡洛爾案所涉及的是某駁船因拴系不牢,在脫錨后碰撞、損壞碼頭中其他船隻的情形;案件的核心問題是如何確定該船船主有無過失。
漢德法官就此提出了以下見解:
由於任何船隻都有脫錨的可能,並在脫錨后對附近的船隻構成威脅,一位船主防止此類事件發生的義務應由三個變數來決定:(1)該船脫錨的可能性(probability,簡稱P);(2)該船脫錨后將給其他船隻造成的損害(loss或injury,簡稱L);(3)對此採取足夠預防措施將給該船主帶來的負擔(burden,簡稱B)。
漢德法官所提出的上述公式(因其所涉及的B、P、L變數,又稱BPL公式)隨後成為美國各級法院在侵權案件中經常使用的判定過失有無的標準。根據漢德公式的表述,法院經常以B、P、L來計算當事人應當採取的對他人人身和財產安全的“合理關注”(reasonable care)。如果採取足夠預防措施(如,在上述河水污染的例子中,對將被排放的廢水做充分的凈化)將給當事人帶來的負擔(B)大於造成有關損害的概率(P)與有關損害(L)的乘積,當事人便不必採取預防措施,因為由法律要求當事人這樣做(花費較多的費用,如1,000美元,以杜絕較少的概率損失[即P與L的乘積;而不是單純的L],如900美元)從經濟上講是不合理、無效率的,超出了“合理關注”的範圍。但是,倘若B小於或等於P與L的乘積(如可用900美元的代價來防止1,000美元的概率損失),而當事人卻未採取足夠的預防措施,該當事人將被認定存在過失。
如上所述,經濟效率和實用主義(utilitarianism)。但這一公式更富有啟發性的實際上是它隱含的社會觀(view of society)。漢德公式在某種意義上把一個侵權案件中的原、被告當成了一個整體:正如同要求原告本身用1,000美元的花費去消除原告本身900美元的概率損失無疑是不合理的,漢德認為,要求被告用1,000美元的花費去消除原告900美元的概率損失也同樣是不合理的,因為兩者最終招致的同樣是100美元(1,000美元-900美元)的凈損失。這無形中把原、被告看作了一個整體,“統一結算”;也進而把社會看成了一個整體,不再要求社會--經由法律--對被告施加過失責任(因為倘若如此,便是給社會造成100美元的凈損失)。
不過,雖然漢德公式在理論上頗具說服力,在實際應用時,該公式經常遇到B、P、L無法真正量化的問題。以P和L為例,人們通常很難確切地計算出某一事故發生的可能性以及該事故將造成的損失。實際上,一起事故所能造成的損失很可能輕重不一;而造成不同損失的可能性又會隨損失的輕重不同而不同。這些不確定因素的存在因而增加了人們在實踐中應用漢德公式或其他類似標準的難度。
雖然無論在美國還是在其他國家,上述公式仍只被局限於侵權法領域的過失侵權制度,著者認為,該公式可以被引申、借用到我國的行政法領域,對行政罰款的確定提供重要、有效的指導。具體說來,在確定行政罰款的標準和具體數額時,我國的有關機構可以參照漢德公式的做法,針對一件行政罰款案,對其所涉及的B(即預防有關損害發生所需要的費用)、P(有關損害發生的概率)、L(有關損害)這三個變數及其相互關係做出認定,在此基礎上選擇、確定應收取罰款的具體數額。通過集中考慮這三個變數,行政罰款將獲得比“過罰相當”原則所能提供的更紮實、更合理的依據,而不再是“無章可循”。
之所以選擇漢德公式來協助改進我國的行政罰款制度,是因為在著者看來行政罰款的理論前提恰巧與漢德公式所隱含的社會觀(如上所述)彼此相容。不論其目前的實行狀況如何,著者以為,行政罰款的理論前提都應是以政府為整個社會的代表和委託管理者,統籌考慮,理性地消除或減少--根據社會所制定的法律法規--對社會有害的違法違規行為。因此,行政罰款的首要目的是在有關損害實際發生前,對可造成該損害的違法違規行為進行事前的遏止;而當損害一旦發生,則應主要由侵權法來確定事後的法律責任、賠償數額等一系列事宜。對有關個人和組織處以罰款的目的,應是促使他們對自己有可能損害他人的行為做出恰當的成本效益分析,杜絕對自己也對他人不利的有害行為。行政罰款的標準和具體數額的確定,應以此為出發點。
漢德公式雖然出自侵權法,卻意在裁定在有關損害發生前,被告是否本應採取預防措施,防止該損害的發生。因此,漢德公式選取的時間框架恰巧是行政罰款所面對的時間框架。該公式所考慮的變數P與L的乘積也正是為行政罰款所關注、由違法違規行為造成的實際危險;而變數B則是政府代表社會決定是否消除或減少某一危險時必須考慮的成本因素。所以,在明確行政罰款的首要目的的前提下,對B、P、L三個變數的掌握應能幫助有關機構在實施行政罰款時更精確地裁定罰款數額,使行政罰款更有效地實現其目的和功能。
行政機構(或有關立法部門)應通過各種方法確定B、P、L的數值。如上所述,變數B所代表的是預防有關損害發生所需要的費用。有關B的數據通常可以由相關的行業組織或科研單位提供。以上述河水污染的情形為例,B的數值將是對工廠甲所需排放廢水事先進行充分凈化所需的購買、安裝和使用相應設備的費用(包括相關的人工費)等。這一數據通常可由化工部門和/或對口的科研機構、行業組織提供、論證,在大多數情況下都可以做到較為具體、精確。有關廢水的安全排放標準以及某些其他可罰款事項的相應標準可遵循現有和將適時制定的國家標準和/或適用的地方標準。
相比之下,對變數P和L數值的計算可能會相對複雜。有關P和L數據的一個主要來源是法院等對以往類似損害的處理。對絕大多數損害類型來講,法院等部門對以往案件的審理應已包含足夠的有關數據;有關部門可據此對同類損害的平均發生概率、程度和範圍等做出相當可靠的估計,從而計算出概率損失的數值。譬如,河水污染的例子中,以往污染給有關動植物(如魚苗等)甚至人類帶來的損害及其發生頻率應能對類似損害在將來的發生概率等提供較為可靠的線索。此外,由具體部門(如當地環境保護局)和/或科研單位等對有關廢水的生化檢驗也應能提供重要的相關數據(如一定量的廢水可致多少魚苗死亡等等)。
在確定B、P、L三個變數的數值時,有關部門應通過調查研究、聽證等形式充分地聽取有關各方(如行業主管部門、科研單位、專家、從事有關損害預防的企業或個人、所涉及的兩方或多方當事人包括將要受罰的單位和個人以及有可能受害的單位和個人)的意見和論證,並對各方的意見和論證做充分的比較與權衡,以期做出盡量準確、合理、通常適用於同一種類的多個個案(而不是僅僅針對一個孤立個案--否則將增加資源浪費和不可行性)的計算。
以上對B、P、L數值的計算可以被行政機構(或有關立法部門)直接用來確定有關行政罰款的數額。根據社會(經由政府)對概率損失所要達到的遏止程度,以B、P、L來確定行政罰款的數額可以大致分為三種情形。
為實現行政罰款事先遏止有關損害這一首要目的,有關機構需要確定其對概率損失所要達到的遏止程度。在這一方面,有關機構主要面對以下三種選擇。第一種選擇是促使當事人不惜任何代價來防止一切損害的發生;第二種選擇是只在防止損害所需付出的代價小於或等於概率損失(即B≤PL)的情況下才促使當事人防止損害的發生,即允許有效率的損失或損害(efficient loss or injury);除此之外,有關機構也可以設計出某種折衷方案,例如要求當事人在防止損害所需付出的代價大於概率損失的情況下也要防止損害的發生,但對該代價與該概率損失之間的比率加以某種限定(如在該代價超出該概率損失兩倍的情況下,即B>2PL時,便不再要求當事人防止損害的發生)。
在絕大多數情況下,有關機構應考慮以上述第二種選擇作為其政策取向,即:只在防止損害所需付出的代價小於或等於概率損失的情況下才促使當事人防止損害的發生。這樣做,可以最大限度地實現社會的經濟效益、理性地消除或減少損害的發生。在防止損害的成本小於概率損失(如B=9,000元,PL=10,000元)時,免除損害的發生可使社會在總體上得到正面的經濟效益(PL-B=10,000元-9,000元=1,000元)。在防止損害的成本等於概率損失(如B=10,000元,PL=10,000元)時,雖然免除該損害不能帶來正面的經濟效益(PL-B=10,000元-10,000元=0元),但是,由於這樣做可以--在不浪費社會資源的情況下--同時減輕或消除人們對損害發生的擔憂等負面情緒,從而實現額外的社會效益,所以要求當事人免除該損害的發生仍不失為一種理性的選擇。
在某些情況下,由於社會道德觀念、公眾要求等因素,有關部門也可以不排除採用上述其他兩種(尤其是第三種)做法,即:在防止損害所需付出的代價大於概率損失的情況下同樣要求當事人防止損害的發生。但是,在採取這種做法之前,有關部門必須認識到:在通常情況下,防止損害所需付出的代價最終都是由公眾、由社會來承擔的(例如,在上述河水污染的例子中,對工廠甲的罰款將不可避免地作為其生產成本的一部分,相應地提高其產品的價格,從而被轉嫁到其用戶或消費者身上)。所以,嚴格地講,在防止損害所需付出的代價遠大於概率損失的情形下(如B≥2PL時),仍要求當事人防止損害的發生將很少能給社會帶來正面的效益。
如以B、P、L來表示,在上述三種情形下,對有關行政罰款的確定應分別依照以下公式進行:
1、如要促使當事人不惜任何代價來防止一切損害的發生:無論B與PL的相互關係如何(即:無論B<、=或者>PL),對未能採取措施、防止有關損害發生的當事人均應處以罰款,罰款額應略大於B,使其等於B加上因實施行政罰款而產生的相應的行政開支(如上述為取得有關B、P、L的數據而進行的調查研究和聽證的費用,以及下文將要提到的招標的費用等)。
如對某一可罰款事項採用這一政策,有關部門將只需取得有關B的數據,對P與L將無須理會。但是,如上所述,這種做法至少在B遠大於PL的情形下會給當事人乃至公眾造成不合理、無效率的負擔,所以在絕大多數情形下並不是一種正確的政策選擇。
2、如只在B小於或等於概率損失的情況下才促使當事人防止損害的發生:行政機構應只在B≤PL時對當事人處以罰款,罰款額應略大於B,使其等於B加上因實施行政罰款而產生的相應的行政開支。B>PL的情形應在實際損害發生后,由法院、仲裁委員會等訴訟機構按照侵權法等適用法律法規處理或者這可能也是更合理、更有效率的做法--由相應的社會保險機制處理。
3、如採用上述的某種折衷方案(如在B超出概率損失1.5倍的情況下便不再要求當事人防止損害發生):有關機構應只在規定的情形下(如B≤1.5PL時)對當事人處以罰款,罰款額應略大於B,使其等於B加上因實施行政罰款而產生的相應的行政開支。B>1.5PL的情形應在實際損害發生後由法院、仲裁委員會等按照侵權法等適用法律法規處理或由相應的社會保險機制處理。
根據可罰款事項的不同,有關政府機構顯然可以對不同事項採取不同的遏止政策:如對絕大多數事項採取上述第2種政策;對少數事項採取第3種政策;但也不排除對極個別事項(如可導致某種嚴重傳染病流行的違法違規行為)採取第1種政策,不惜一切代價儘力杜絕。