相似理論
各相似現象相似原理的學說
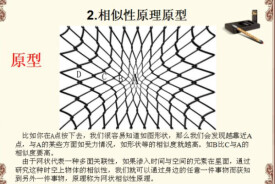
相似理論,是說明自然界和工程中各相似現象相似原理的學說。是研究自然現象中個性與共性,或特殊與一般的關係以及內部矛盾與外部條件之間的關係的理論。在結構模型試驗研究中,只有模型和原型保持相似,才能由模型試驗結果推算出原型結構的相應結果。
似論指導模型試驗,確“模型”“型”似程、級。隨計算技術斷步,似論模型試驗論繼續存,且步擴充範圍領域,計算“仿”領域指導論。隨“似”概念益擴,似論科領域擴展包括濟、社科及思維科哲領域趨勢。
似論展規律(程)件(件),數理方程所固有的在量綱上的齊次性以及數理方程的正確性不受測量單位制選擇的影響等為大前提,通過線性變換等數學演繹手段而得到了自己的結論。相似理論的特點是高度的抽象性與寬廣的應用性相結合,相似理論的內容並不多,甚至不被當作一個單獨的學科。相似理論是試驗的理論,用以指導試驗的根本布局問題,它為模擬試驗提供指導,尺度的縮小或放大,參數的提高或降低,介質性能的改變等,目的在於以最低的成本和在最短的運轉周期內摸清所研究模型的內部規律性。相似理論在現代科技中的最主要價值在於它指導模型試驗上。儘管相似理論本身是一個比較嚴密的數理邏輯體系,但是,一旦進入實際的應用課題,在很多情況下,不可能是很精確的。因為相似理論所處理的問題通常是極其複雜的。
似論賴存基礎:
(1)現象相似的定義;
(2)自然界中存在的現象所涉及到的各物理量的變化受制於主宰這種現象的各個客觀規律,它們不能任意變化;
(3)現象中所涉及的各物理量的大小是客觀存在的,與所採用的測量單位無關。
(1)相似及相似常數
如果原型和模型相對應的各點及在時間上對應的各瞬間的一切物理量成比例,則兩個系統相似。相似常數(也稱為相似比、比尺、模擬比、相似係數等)是模型物理量同原型物理量之比。主要有幾何相似比、應力、應變、位移、彈性模量、泊松比、邊界應力、體積力、材料密度、容重相似比等。在這些相似常數中,長度、時間、力所對應的相似常數稱為基本相似常數。
(2)相似指標及相似判據
模型和原型中的相似常數之間的關係式稱為相似指標。若兩者相似,則相似指標為1。由相似指標導出的無量綱量群稱為相似判據。
(3)同類物理現象
具有相同的物理內容,並能用同一微分方程描述的物理現象。如果兩個物理現象的微分方程的形式一樣,但物理內容不同,就不是同類物理現象。
(4)時間對應點
是指從起始時刻起,具有的瞬時,不是從起始時刻起具有相同時間的點。
(5)空間對應點
顯然只有幾何相似的體系才具有空間對應點,它是物理現象相似的前提。

相似理論
相似第一定理:兩個相似的系統,單值條件相同,其相似判據的數值也相同。
相似第三定理:凡具有同一特性的現象,當單值條件(系統的幾何性質、介質的物理性質、起始條件和邊界條件等)彼此相似,且由單值條件的物理量所組成的相似判據在數值上相等時,則這些現象必定相似。
這3條定理構成了相似理論的核心內容。相似第三定理明確了模型滿足什麼條件、現象時才能相似,它是模型試驗所必須遵循的法則。